Una de las habilidades más importantes en matemáticas es saber cómo leer e interpretar un gráfico, particularmente cuando se estudia el tema de funciones. A menudo, las funciones están representadas por un diagrama o algún gráfico, de ahí la importancia de interpretar los datos que tiene frente a usted para poder analizarlos y sacar conclusiones. De hecho, saber leer información de un gráfico o tabla no es una "ciencia espacial". Esta es una habilidad adquirida, que requiere la comprensión de una serie de normas básicas y prácticas. En el presente artículo encontrarán una serie de herramientas que les permitirán "sumergirse" en el tema con el pie derecho.
Lectura de información de gráficos
¿Qué es un gráfico?
Un gráfico es básicamente cualquier representación en el sistema de coordenadas que permite que los datos se transmitan de forma visual y accesible (para una explicación más detallada, consulte el artículo dedicado "gráfico ")
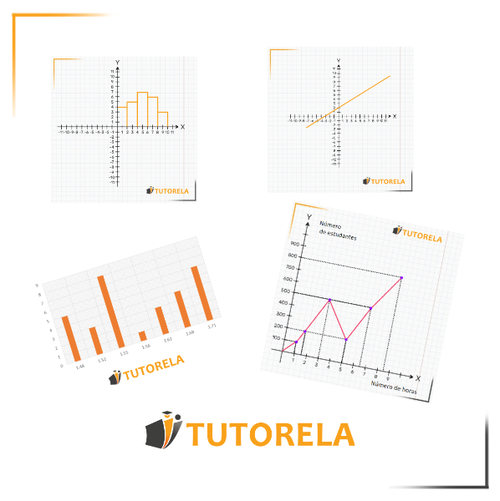
Tipos de gráficos
Existen varios tipos de gráficos:
- Gráfica discreta (para obtener una explicación más detallada, consulte el artículo dedicado " Gráfica discreta ") cuya forma más común es un diagrama de barras.
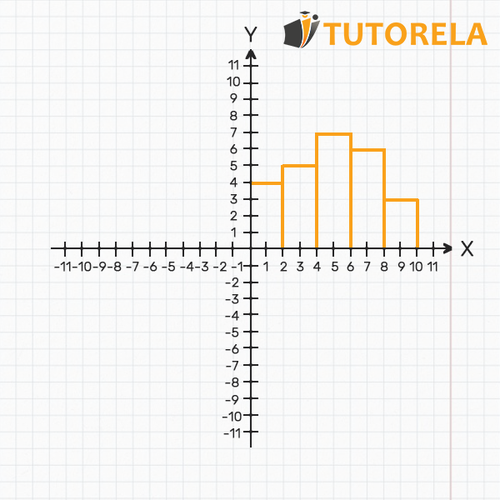
Gráficos continuos (para obtener una explicación más detallada, consulte el artículo dedicado " Gráficos continuos "), que como su nombre implica es una línea continua de valores en el plano cartesiano.
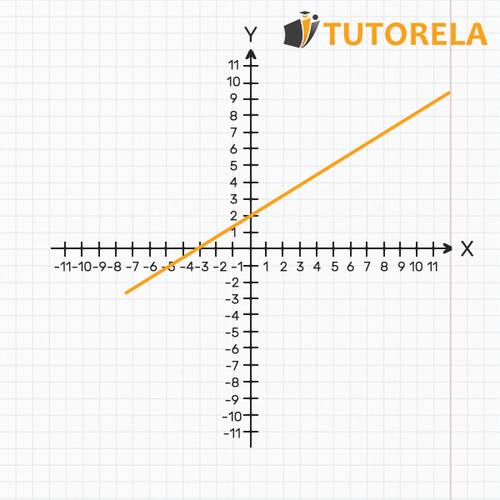
¿Qué es una tabla de valores?
Una tabla de valores (para obtener una explicación más detallada, consulte el artículo dedicado " Tabla de valores ") generalmente tiene como objetivo resumir los datos en los que se basa el gráfico, ya sea una gráfico discreto o continuo.
Ejemplo de una tabla de valores para
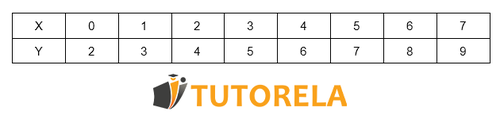
Si estás interesado en más información sobre "gráficos" puedes encontrar información detallada en los siguientes artículos:
Recolección y organización de datos - investigación estadística
Representación gráfica de una función
En la página web de Tutorela encontrarás una variedad de artículos con interesantes explicaciones sobre matemáticas
Ejemplos y prácticas de lectura e interpretación de la información dentro de un gráfico
Ejercicio 1
El siguiente gráfico de líneas muestra el número de estudiantes en la universidad desde el momento en que se abren sus puertas.
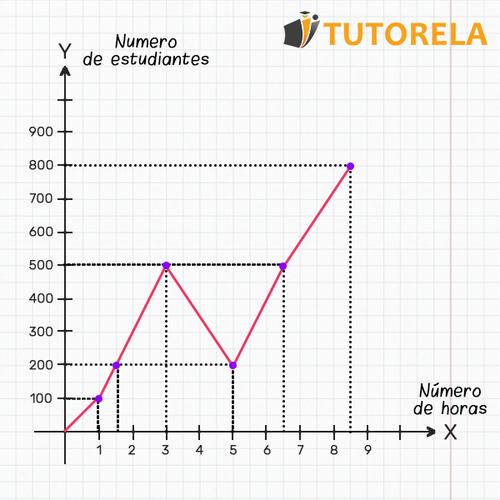
Según el gráfico, respondan las siguientes preguntas
- ¿Cuántos estudiantes había en la universidad al cabo de una hora?
- ¿Cuántos estudiantes había en la universidad al cabo de tres horas?
- ¿Después de cuántas horas había 500 estudiantes en la universidad?
- ¿Después de cuántas horas había 200 estudiantes en la universidad?
Solución:
Antes de abordar la solución de cada una de las preguntas es necesario entender bien qué representa cada uno de los ejes que tenemos ante nosotros:
El eje representa el tiempo en horas desde el momento en que abre la universidad, mientras tanto el eje representa el número de estudiantes en la universidad como función del tiempo en horas.
- Para resolver esta consigna, observaremos la gráfica y encontraremos en el eje el valor que representa una hora. Ahora trazaremos una línea discontinua desde el valor a la dirección del gráfico. En el siguiente paso, trazaremos una línea discontinua desde el punto del gráfico hacia el eje y veremos que el valor que obtenemos es . Es decir, significa que al cabo de una hora había estudiantes en la universidad.
- Repetiremos la acción que realizamos en la sección anterior. Observemos el gráfico y encontremos en el eje el valor que representa tres horas. Ahora trazaremos una línea discontinua desde el valor a la dirección del gráfico. A continuación, trazaremos una línea discontinua desde el punto del gráfico hacia el eje y veremos que el valor que obtenemos es . Es decir, al cabo de tres horas, la universidad tenía estudiantes.
- En la presente sección tendremos que actuar al revés. Observaremos la gráfica y encontraremos en el eje el valor que representa el número de estudiantes. Ahora trazaremos una línea discontinua desde el valor a la dirección del gráfico. Encontraremos dos puntos coincidentes en el gráfico. En el siguiente paso, trazaremos una línea discontinua desde cada uno de los puntos de la gráfica hacia el eje y se podrá ver que los valores que obtenemos son y . Es decir, que la universidad tenía alumnos a las horas y a las horas.
- Repetiremos la acción que realizamos en la sección anterior. Observemos la gráfica y encontremos en el eje el valor que representa el número de estudiantes. Ahora trazaremos una línea discontinua desde el valor a la dirección del gráfico. Encontraremos dos puntos coincidentes en el gráfico. A continuación, trazaremos una línea discontinua desde cada uno de los puntos de la gráfica hacia el eje y por lo tanto los valores que obtenemos son y . Es decir, significa que la universidad tenía estudiantes después de horas y después de horas.
Respuesta:
- estudiantes
- estudiantes
- Después de horas y después de horas
- Después de horas y después de horas
Ejercicio 2 - de lectura de información de un gráfico
El diagrama de barras que se presenta a continuación describe el número de residentes de la ciudad que participaron en las actividades organizadas por el municipio de Ibarra, Ecuador, por cada tipo de actividad realizada.
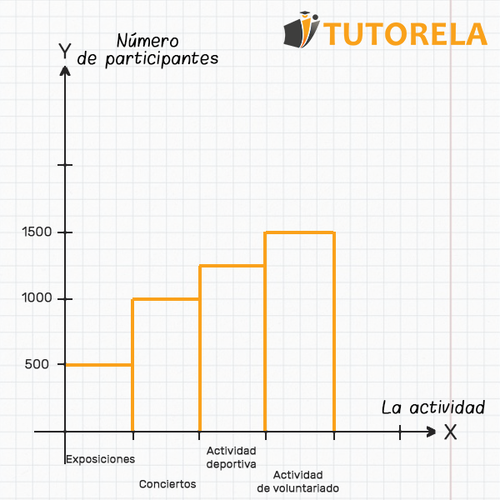
Ejercicios de lectura de información de gráficos
Ejercicio 1
Consigna
En el gráfico de la función lineal que pasa por los puntos y
Hallar la pendiente de la gráfica.
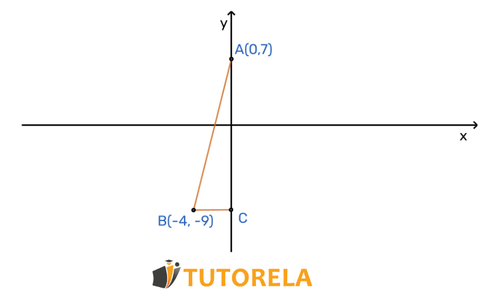
Solución
Reemplazamos según los datos existentes
Respuesta
Ejercicio 2
Consigna
Una gráfica de una función lineal pasa por los puntos
Solución
Usamos la fórmula de la pendiente
Reemplazamos en consecuencia los datos
Si la pendiente es igual a , entonces la pendiente es positiva y la función ascendente
Respuesta
Ejercicio 3
Consigna
La gráfica de la función lineal pasa por los puntos
¿La función es: creciente, decreciente o constante?
Solución
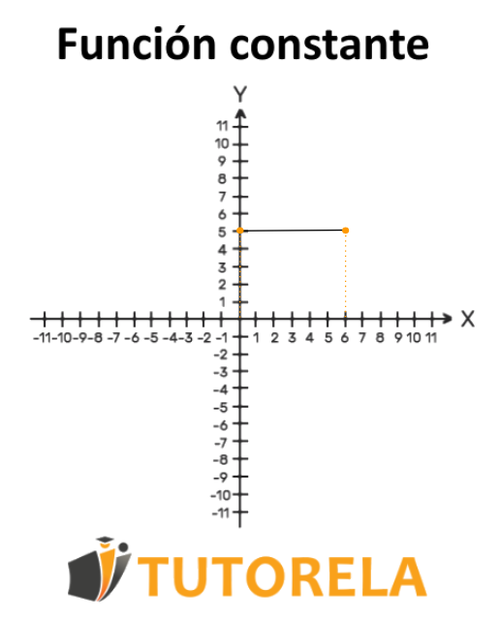
Respuesta
La función es una función constante.
Ejercicio 4
Consigna
La gráfica de la función lineal pasa por los puntos
Solución
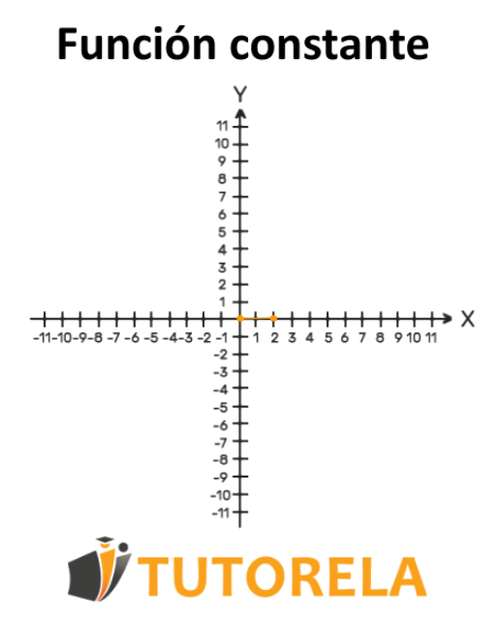
Respuesta
Función constante
Ejercicio 5
Consigna
¿En qué punto el gráfico de la primera función se cruza con el gráfico de la segunda función II?
Solución
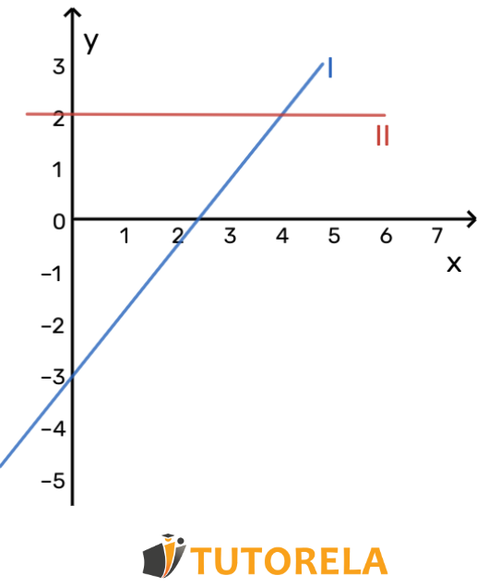
Respuesta
preguntas de repaso:
¿Cómo interpretar los resultados de gráficos estadísticos?
Un gráfico estadístico nos mostrará datos cuantitativos que fueron recolectados, por ello es muy importante identificar qué tipo de gráfico estamos trabajando, estos pueden ser: un diagrama de barras, gráfica de porcentajes, gráficas de estadística, gráfica de histogramas y de ahí la importancia de saber leer e interpretar la información que nos está dando dicho gráfico, ya sea en el eje y en el eje , en el caso de un diagrama de barras o un histograma, para poder analizarlos e interpretarlos y así llegar a una conclusión.
¿Cómo interpretar un gráfico de barras?
Primero que nada debemos de ubicar el eje y el eje , posteriormente observaremos qué datos nos indican estos, y de esa forma poder leer los datos y relacionarlos con los datos de cada eje y llegar a una conclusión.
Gráfica de barras ejemplo
Consigna
En el siguiente diagrama de barras se representa las estaturas de alumnos
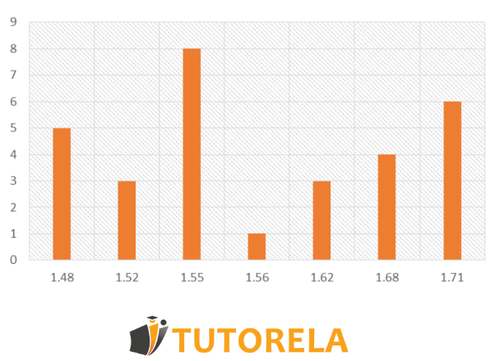
Solución:
Podemos observar en el gráfico que en el eje se representan las estaturas obtenidas y en el eje podemos observar el número de alumnos que registraron esas estaturas
Ejemplo, podemos observar que la estatura de m si trazamos una línea hacia arriba podemos ver que llega en el en el número . Esto lo podemos interpretar como: alumnos registraron esa estatura.
En el x la estatura de m podemos relacionarla con el número en eje , esto quiere decir que alumnos tiene la estatura de m. y de esta forma podemos seguir interpretando los datos que nos proporciona dicho gráfico.
¿Cómo se lee un gráfico?
Primero debemos de determinar qué tipo de gráfico se nos está presentando, una vez identificado esto, por ejemplo si se trata de un histograma, deberíamos de observar qué datos tenemos en los ejes de coordenadas y analizarlos para interpretar dichos datos.
¿Cómo se interpreta un gráfico de líneas?
Normalmente un gráfico de líneas nos indicará cambios que se van dando usualmente en función del tiempo y distancia, entonces primero deberíamos de observar qué datos se nos presenta en los ejes coordenados para poder interpretar los datos que se estudiarán.
¿Qué debemos de tener en cuenta en los gráficos de barras?
Para poder analizar los datos en una gráfica de barras es importante tomar en cuenta los datos que nos están proporcionando en el eje y en el eje , y así interpretar de una mejor manera la información que se nos proporciona.
- Valor absoluto y desigualdad con valor absoluto
- Sistema de coordenadas
- Par ordenado
- Gráfico
- Lectura de información de gráficos
- Tabla de valores
- Gráfica discreta
- Gráfica continua
- Método algebraico
- Factorización: Extracción de factor común
- La propiedad distributiva: ampliación
- Desigualdades
- Inequations (con valor absoluto)
- Función lineal
- Representación gráfica de una función que representa una proporcionalidad directa
- La función lineal y=mx+b
- Hallar ecuación lineal
- Positividad y negatividad de una función lineal
- Representación de fenómenos usando funciones lineales
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones








