La gráfica continua es la versión clásica de lo que llamamos "gráfico", y es un tema muy importante que reaparece en casi todos los temas de matemáticas.
Gráfica continua
¿Qué es una gráfica continua?
Una gráfica continua es una gráfica lineal que describe la continuidad de los números a lo largo del eje horizontal X.
Cada punto de la gráfica continua se puede representar mediante un par ordenado donde el valor de la izquierda entre paréntesis representa el valor numérico del eje horizontal, mientras tanto el valor de la derecha entre paréntesis representa el valor numérico del eje vertical.
A continuación un ejemplo de gráfica continua
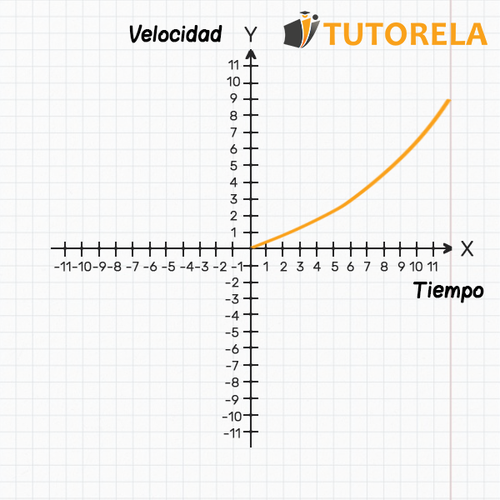
- En este gráfico, el eje representa el tiempo, mientras tanto el eje representa la velocidad.
- El eje representa un valor continuo de tiempo y observamos en el gráfico cómo cambia la velocidad en función del tiempo.
A veces las gráficas parecen complicadas, pero si entendemos cómo funcionan veremos que, en realidad, son muy simples. Una gráfica es sólo una manera de mostrar mucha información de una vez.
Tenemos varios tipos básicos de gráficas. En este artículo conoceremos las gráficas discretas
Otro y diferente ejemplo
Ejemplo 1
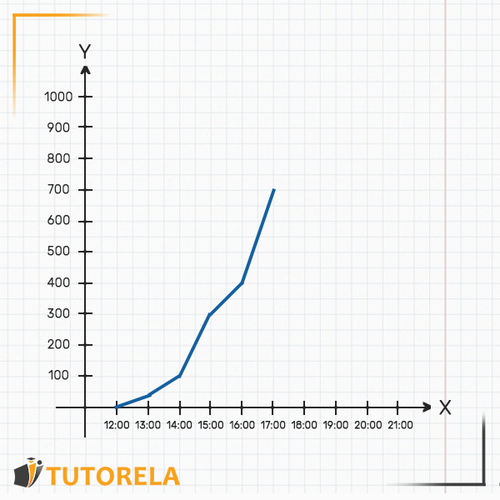
Toda gráfica se compone de dos ejes: el eje y el eje . El eje es el horizontal (podemos imaginarlo como el suelo de la gráfica). En esta gráfica el eje indicará la hora. Es decir, a medida que nos movamos sobre el eje la hora avanzará.
Por ejemplo, podrás identificar dónde se ve la hora , luego (a su derecha), la y así sucesivamente.
El eje es el vertical (podemos imaginarlo como la pared de la gráfica). En este caso representa la cantidad de litros de agua que hay en la piscina en cada momento.
Con los dos ejes, esta gráfica describe la cantidad de agua que va habiendo en la piscina a medida que transcurren las horas. Es decir, la piscina se va llenando de agua con el pasar del tiempo y la gráfica muestra la cantidad de agua que hay en cada momento dado.
A veces las gráficas parecen complicadas, pero si entendemos cómo funcionan veremos que, en realidad, son muy simples. Una gráfica es sólo una manera de mostrar mucha información de una vez.
Tenemos varios tipos básicos de gráficas. En este artículo conoceremos la gráfica continua, aprenderemos a leerla y dibujarla.
Ejemplo 1: (Seguiremos con el último ejemplo)

Toda gráfica se compone de dos ejes: el eje y el eje . El eje es el horizontal (podemos imaginarlo como el suelo de la gráfica). En esta gráfica el eje indicará la hora. Es decir, a medida que nos movamos sobre el eje la hora avanzará. Por ejemplo, podrás identificar dónde se ve la hora , luego (a su derecha), la y así sucesivamente.
El eje Y es el vertical (podemos imaginarlo como la pared de la gráfica). En este caso representa la cantidad de litros de agua que hay en la piscina en cada momento.
Con los dos ejes, esta gráfica describe la cantidad de agua que va habiendo en la piscina a medida que transcurren las horas. Es decir, la piscina se va llenando de agua con el pasar del tiempo y la gráfica muestra la cantidad de agua que hay en cada momento dado.
Intenta deducir:
- ¿Cuántos litros había en la piscina a las ?
- ¿Cuándo hubo exactamente litros en la piscina?
- ¿Cuánta agua había en la piscina a las ?
Respondamos las preguntas:
1.Para comprender cuánta agua había en la piscina a las en punto, buscaremos sobre el eje dónde está la hora , luego, veremos dónde está la gráfica sobre el eje a dicha hora. En este caso podremos ver que, a las había litros de agua en la piscina. Es decir, a esa hora comenzaron a llenarla.
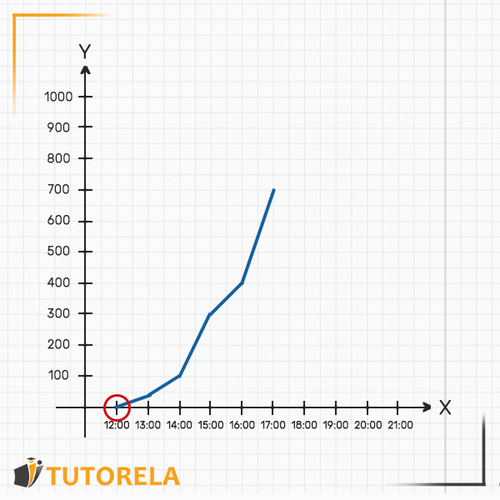
2.Para averiguar cuándo hubo exactamente litros en la piscina buscaremos sobre el eje la marca que indica 300 litros. Podemos incluso apoyar el dedo sobre dicho punto en el eje . Luego comenzaremos a desplazarnos hacia la derecha sobre el eje (moviendo nuestro dedo) hasta encontrarnos con la gráfica. Nos percataremos de que el punto de encuentro con la gráfica queda exactamente encima de la hora (señalado en la siguiente gráfica). Es decir, a las en punto había en la piscina litros de agua exactamente.
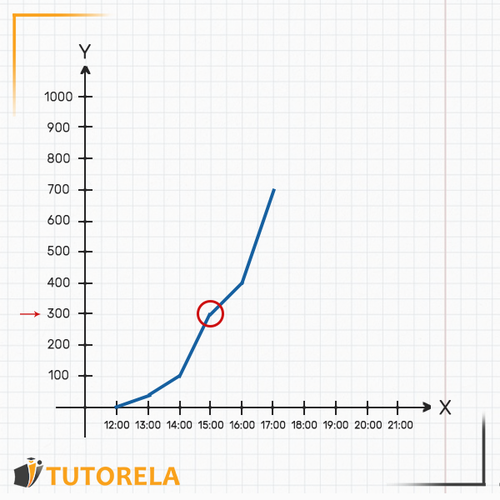
3.La pregunta cuestionada fue ¿cuánta agua había en la piscina a las ? La hora no aparece en la gráfica, pero nosotros sabemos que se encuentra justo en el medio entre las y las . Claramente podremos deducir dónde se vería la hora sobre el eje .
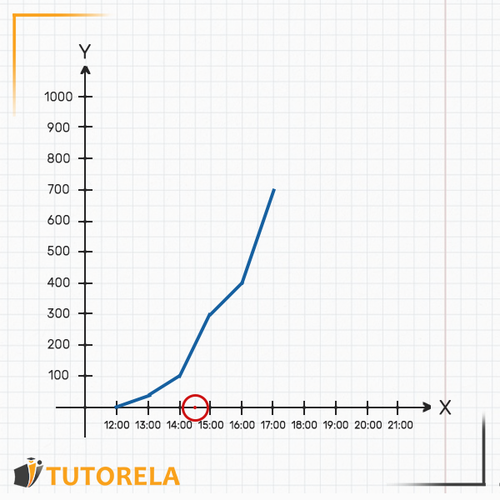
Ahora podemos averiguar cuánta agua había en la piscina a esa hora: veamos dónde se encuentra la gráfica en relación con el eje justo a la hora .
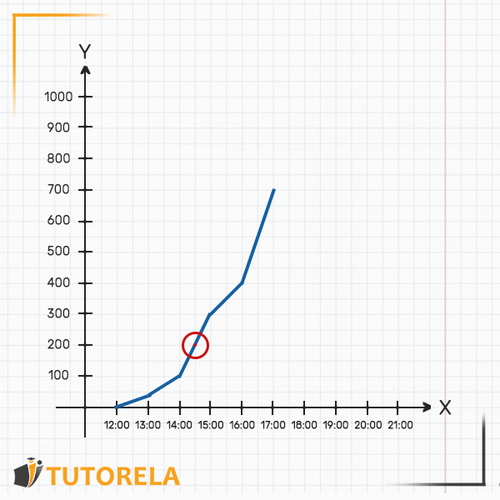
Es decir, a las había en la piscina litros de agua exactamente.
Qué significa gráfica continua
En el artículo anterior hemos tratado el tema de la gráfica discreta. En el ejemplo reciente y en los que se encuentran a continuación vemos casos de gráfica continua. ¿A qué nos referimos cuando escribimos gráfica continua?
Una gráfica continua es una gráfica lineal que describe continuidad numérica sobre el eje horizontal . Por ejemplo, el agua al llenar una piscina (el ejemplo recién visto). El significado de la palabra «continuo» es que no tiene interrupciones, o sea hay continuidad de datos. Por lo tanto, podremos deducir exactamente cuánta agua hay en la piscina en cualquier momento.
Ejemplo 2 - Otro ejemplo de gráfica continua
Un coche parte a las de Madrid hacia Barcelona. Cuando arriba se detiene. La gráfica describe la distancia recorrida por el coche desde su punto de partida.
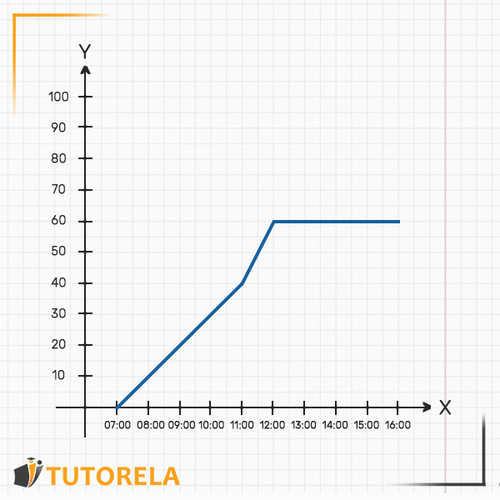
- ¿Cuán distante está el coche de Madrid a las ?
- ¿Cuán distante está el coche de Madrid a las ?
- ¿A qué hora llegó el coche a su destino?
Solución:
1.Para averiguar la distancia que hay entre el coche y Madrid a las debemos hallar la hora sobre el eje , luego veremos dónde se encuentra la gráfica de la función en relación con dicha hora sobre el eje . En este caso el coche se encuentra exactamente a de distancia de Madrid
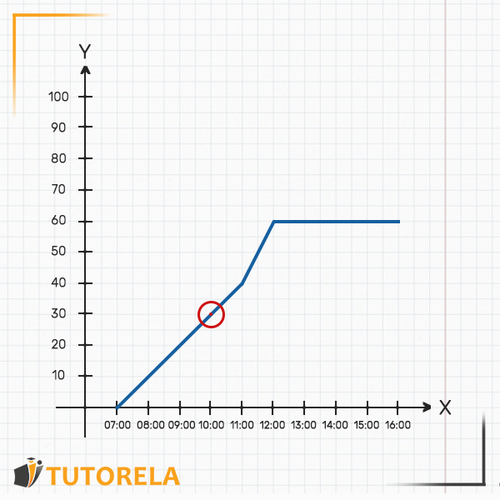
2.La hora no aparece en la gráfica, pero sabemos que está exactamente en el medio entre las y las . Podemos ubicar el lugar preciso y averiguar dónde se traza la gráfica, justo en este punto, en relación con el eje . Deduciremos que el coche se encuentra exactamente a de distancia de Madrid. Es posible llegar a esta deducción debido a que la gráfica es continua.
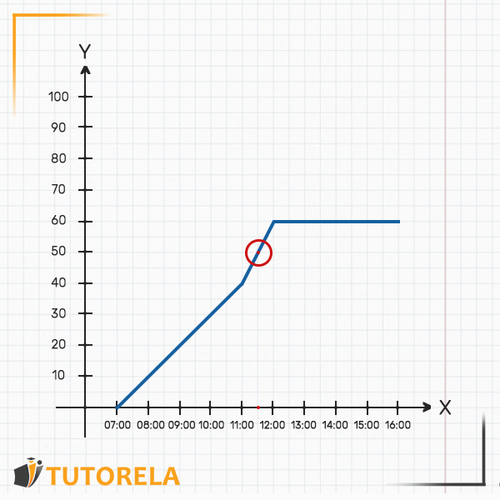
3.¿A qué hora llegó el coche a su destino? No está explícitamente escrita la hora de arribo a destino, sin embargo, se ha explicado que el coche se ha detenido al llegar. Es decir, a partir de cierta hora la distancia que hay entre el coche y Madrid debería fijarse.
Al observar la gráfica veremos que, desde las el coche se mantiene a una distancia constante de Madrid, . Es decir, esa es la hora en la cual el coche arribó a su destino y se detuvo. Se puede ver que también a las y a las el coche sigue estando a de Madrid.
Si estás interesado en más información sobre "gráficos" puedes encontrar información detallada en los siguientes artículos:
Recolección y organización de datos - investigación estadística
Lectura de información de gráficos
Representación gráfica de una función
En la página web de Tutorela encontrarás una variedad de artículos con interesantes explicaciones sobre matemáticas
- Valor absoluto y desigualdad con valor absoluto
- Sistema de coordenadas
- Par ordenado
- Gráfico
- Lectura de información de gráficos
- Tabla de valores
- Gráfica discreta
- Desigualdades
- Inequations (con valor absoluto)
- Función lineal
- Representación gráfica de una función que representa una proporcionalidad directa
- La función lineal y=mx+b
- Hallar ecuación lineal
- Positividad y negatividad de una función lineal
- Representación de fenómenos usando funciones lineales
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones








