Existen 4 criterios para determinar que dos triángulos son congruentes. En este artículo aprenderemos a utilizar el tercer criterio de congruencia:
Criterio de congruencia: Lado, Lado, Lado
Lado, Lado, Lado
Definición: 2 triángulos en los que sus tres lados son de la misma longitud son triángulos congruentes.
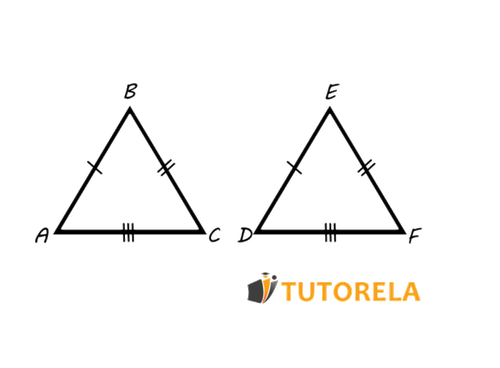
Para demostrar que 2 triángulos son congruentes podemos utilizar uno de los siguientes postulados:
En este artículo estudiaremos este criterio y veremos ejemplos de cómo aplicarlo.
¡Pruébate en lado, lado, lado!
Dado el paralelogramo ABCD
¿Qué se puede decir de los triángulos ACD y ABD?
Ejemplo 1
Dados los triángulos y de modo que
(arista)
(arista)
(arista)
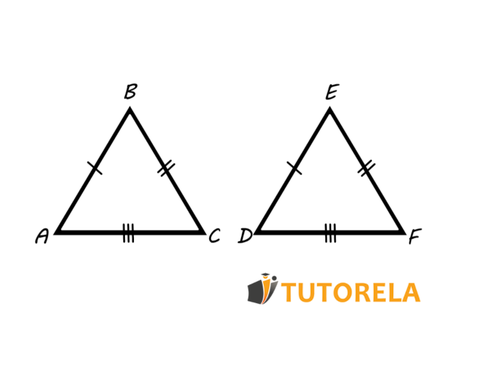
Por consiguiente, deduciremos que: y son triángulos congruentes según el criterio de congruencia de Lado, Lado, Lado.
Lo escribiremos del siguiente modo:
según el criterio de congruencia: Lado, Lado, Lado (LLL)
De lo anterior también deduciremos que:
ya que éstos son ángulos correspondientes e iguales en triángulos congruentes
Ejemplo 2: Ejercicio con congruencia de triángulos
Dados los dos triángulos y de modo que es el lado en común.
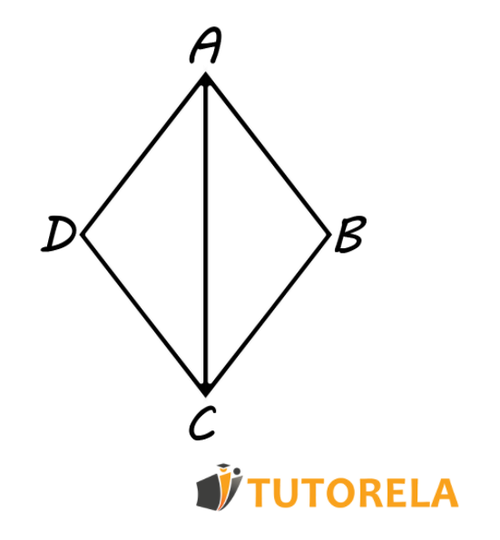
Así mismo se nos informa que:
Demuestra que los triángulos y son triángulos congruentes.
Demostración:
Nos basaremos en el criterio recién aprendido.
Veamos
(arista)
(arista)
Nos percataremos de que (arista) es común a ambos triángulos
De esto se desprende que en los dos triángulos y hay tres pares de lados iguales.
Por consiguiente, podremos deducir que
según el criterio de congruencia Lado, Lado, Lado.
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Criterio de congruencia: Lado, Ángulo, Lado
Criterio de congruencia: Ángulo, Lado, Ángulo
Lado, lado y el ángulo opuesto al mayor de los dos lados
Modo de escritura de la demostración formal en geometría
En la página web Tutorela encontrarás una variedad de artículos sobre matemáticas.
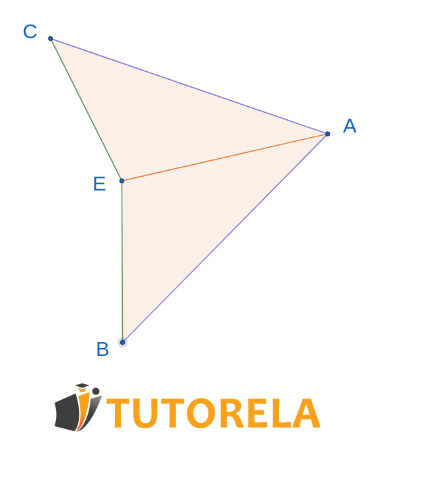
En el dibujo dado:
EC=EB
AC=AB
¿A cuál teorema de congruencia pertenece ΔECA≅ΔEBA?
Dado el paralelogramo ABCD
¿Qué se puede decir de los triángulos ACD y ABD?
Ejercicios de criterio de congruencia: Lado, Lado, Lado
Ejercicio 1
Consigna
En la figura dada:
¿Según qué teorema se superponen los triángulos ?
Solución
Dado que
Dado que
Lado común
Los triángulos congruentes según
Respuesta
Superpuestos
Ejercicio 2
Consigna
En un triángulo isósceles trazamos la altura .
¿De acuerdo con qué teorema de congruencia se superponen los triángulos ?
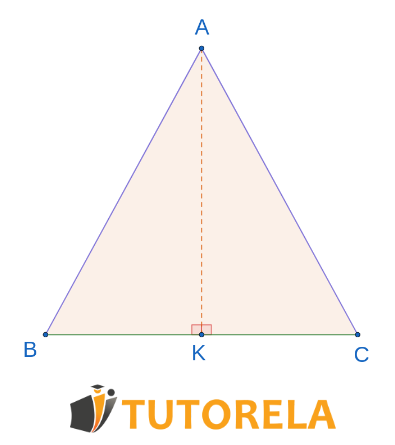
Solución
Dado que el triángulo es isósceles
En un triángulo isósceles, la altura es también una mediana y una mediana corta la base en dos.
Lado común
Los triángulos superpuestos según
Respuesta
Superpuestos según
En el dibujo dado:
EC=EB
AC=AB
¿A cuál teorema de congruencia pertenece ΔECA≅ΔEBA?
Dado el paralelogramo ABCD
¿Qué se puede decir de los triángulos ACD y ABD?
Ejercicio 3
Consigna
Los segmentos y se cruzan en el punto .
¿Según qué teorema de congruencia coinciden los triángulos ?
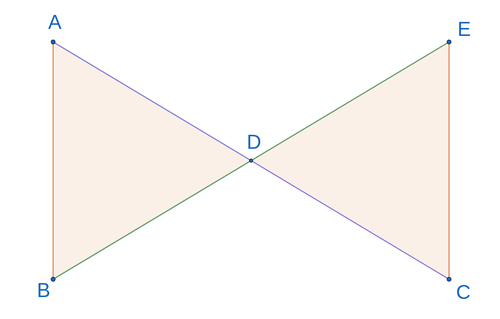
Solución
y
Se cruzan en un punto
intersecta
Ángulos opuestos por el vértice
Triángulos superpuestos según
Respuesta
superpuestos
Ejercicio 4
Consigna
Los triángulos
En el triángulo trazamos la mediana
y en el triángulo trazamos la mediana .
Demostramos:
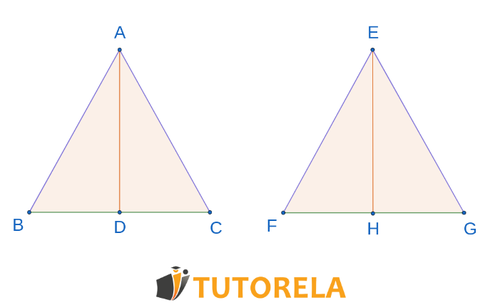
Solución
Dado que los triángulos y son congruentes
En triángulos congruentes las medianas son necesariamente iguales
(saliendo del mismo punto a la misma base)
La mediana cruza la base a la que llega.
Los triángulos congruentes según
Respuesta
Superpuestos según
En el dibujo dado:
EC=EB
AC=AB
¿A cuál teorema de congruencia pertenece ΔECA≅ΔEBA?
Dado el paralelogramo ABCD
¿Qué se puede decir de los triángulos ACD y ABD?
Ejercicio 5
Consigna
Dado el trapecio isósceles .
En su interior contiene el cuadrado .
¿Según qué teorema coinciden los triángulos ?
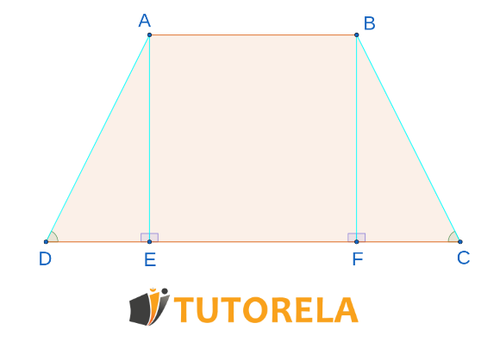
Solución
es un trapecio isósceles (dado)
Trapecio isósceles
Dado que es un cuadrado
Dado que es un cuadrado y todos los lados en un cuadrado son iguales
Los ángulos de la base en un trapecio isósceles son iguales
En un cuadrado todos los ángulos son rectos y miden grados
si dos ángulos son iguales entonces el tercero también es igual
Los triángulos superpuestos según
Respuesta
Preguntas de repaso
¿Qué es el criterio de congruencia de dos triángulos?
Son cuatro los criterios de congruencia de triángulos, estos nos permiten saber si dos triángulos tienen las mismas dimensiones en sus lados y de igual manera la misma longitud de sus ángulos correspondientes, de esta forma podemos decir que los dos triángulos, aun cuando se encuentren en diferente posición u orientación, tendrán la misma forma y medida.
¿Qué es el criterio de congruencia LLL?
Este criterio nos permite deducir si dos triángulos tienen la misma forma y medida, de acuerdo a este criterio dos triángulos son congruentes cuando sus tres lados son iguales.
¿Qué diferencia hay entre el criterio de congruencia LLL y el de semejanza LLL?
El criterio de congruencia por LLL, nos dice que si dos triángulos tienen sus tres lados iguales (Lados congruentes), entonces los dos triángulos son iguales, es decir tienen la misma medida en cuanto a lados y ángulos. Mientras que el de semejanza LLL, nos dice que si dos triángulos son semejantes, entonces sus tres lados son proporcionales, es decir, no tienen la misma medida pero si tienen alguna proporción entre ellos y tienen la misma forma, pero con diferentes medidas en cuanto a sus lados.
¿Qué par de triángulos son semejantes por el criterio LLL?
Dos triángulos van a hacer semejantes cuando tienen la misma forma, sin importar la orientación, es decir, sus ángulos correspondientes miden lo mismo pero sus lados correspondientes no necesariamente miden lo mismo, sino que deben de tener una proporción entre ellos.
¿Cuáles son los criterios de semejanza y congruencia de triángulos?
Criterios de congruencia
Los criterios de congruencia de triángulos son cuatro:
- LAL- Lado, Ángulo, Lado.
- ALA- Ángulo, Lado, Ángulo.
- LLL- Lado, Lado, Lado.
- LLA- Lado, Lado, Ángulo.
Criterios de semejanza
A diferencia de los criterios de congruencia, los criterios de semejanza de triángulos solo son tres:
- LLL- Lado, Lado, Lado.
- LAL- Lado, Ángulo, Lado.
- AAA- Ángulo, Ángulo, Ángulo.
En el dibujo dado:
EC=EB
AC=AB
¿A cuál teorema de congruencia pertenece ΔECA≅ΔEBA?
Dado el paralelogramo ABCD
¿Qué se puede decir de los triángulos ACD y ABD?
ejemplos con soluciones para Lado, lado, lado
Ejercicio #1
Dado el paralelogramo ABCD
¿Qué se puede decir de los triángulos ACD y ABD?
Solución en video
Solución Paso a Paso
Según el teorema lado - ángulo - lado los triángulos son semejantes y coinciden entre sí:
AC=BD Cualquier par de lados opuestos del paralelogramo son iguales
El ángulo C es igual al ángulo B
AB=CD Cualquier par de lados opuestos del paralelogramo son iguales
Por lo tanto todas las respuestas son correctas.
Respuesta
Todas las respuestas correctas
- El Teorema de Pitágoras
- Triángulos congruentes
- Criterio de congruencia: Lado, Ángulo, Lado
- Criterio de congruencia: Ángulo, Lado, Ángulo
- Lado, lado y el ángulo opuesto al mayor de los dos lados
- Congruencia de triángulos rectángulos (en el contexto del Teorema de Pitágoras)
- Suma de los ángulos de un polígono
- Semejanza de triángulos y polígonos
- Semejanza de figuras geométricas
- Razón de semejanza
- Triángulos semejantes
- Criterios de semejanza de triángulos
- Rectángulos congruentes
- Suma de los ángulos internos de un polígono
- Ángulo exterior de un triángulo
- Suma de los ángulos externos de un polígono
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









