Estudiaremos los tres criterios principales de congruencia. Éste es el primero de ellos:
Criterio de congruencia: Lado, Ángulo, Lado
Lado, Ángulo, Lado.
Según este teorema, dos triángulos que 2 de sus lados son respectivamente iguales y el ángulo comprendido entre ellos también es igual, serán triángulos congruentes.
Es importante destacar que el ángulo debe encontrarse entre las dos aristas iguales. Este criterio no se podrá aplicar si se tratara de otro ángulo.
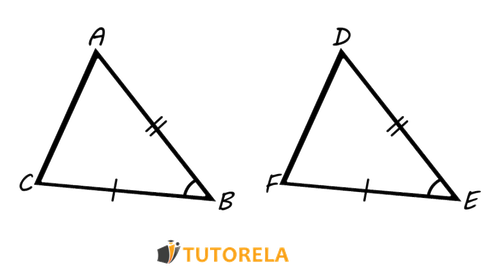
Para demostrar que 2 triángulos son congruentes podemos utilizar uno de los siguientes postulados:
¡Pruébate en lado, ángulo, lado!
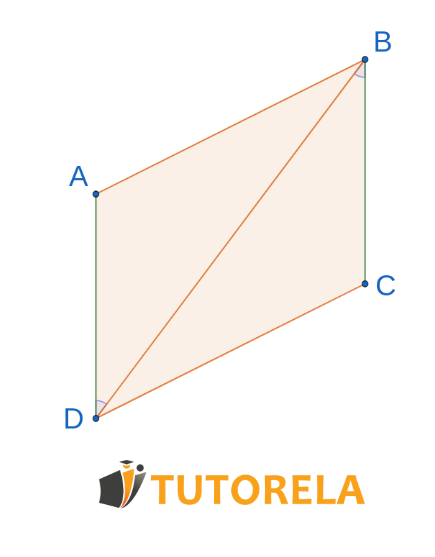
En el dibujo dado:
AB=CD
\( ∢\text{BAC}=∢\text{DCA} \)
¿Según qué teorema, los triángulos Δ ABC ≅Δ CDA son congruentes?
\( \)
Definición de triángulos congruentes
Dos triángulos son congruentes si dos lados y el ángulo comprendido entre ellos, miden lo mismo.
Este criterio nos ayuda a probar que dos ángulos son congruentes.
¡Atención! El ángulo debe ser el que está comprendido entre los dos lados iguales. Este teorema no se podrá aplicar si se tratara de otro ángulo.
Ejemplo 1 (Lado, Ángulo, Lado)
Dados dos triángulos y y los siguientes datos:
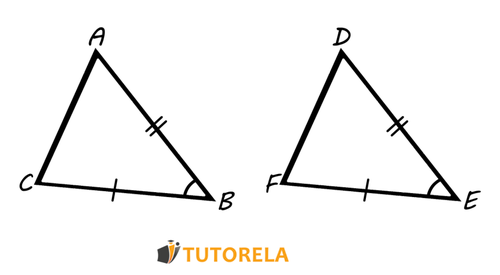
De esto se deduce que los triángulos y son congruentes, por lo tanto, escribiremos:
según el criterio de congruencia Lado, Ángulo, Lado (LAL)
En el dibujo dado:
AB=CD
\( ∢\text{BAC}=∢\text{DCA} \)
¿Según qué teorema, los triángulos Δ ABC ≅Δ CDA son congruentes?
\( \)
Ejemplo 2 - congruencia (Lado, Ángulo, Lado)
Sobre el lado han construido dos triángulos: el y el de modo que:
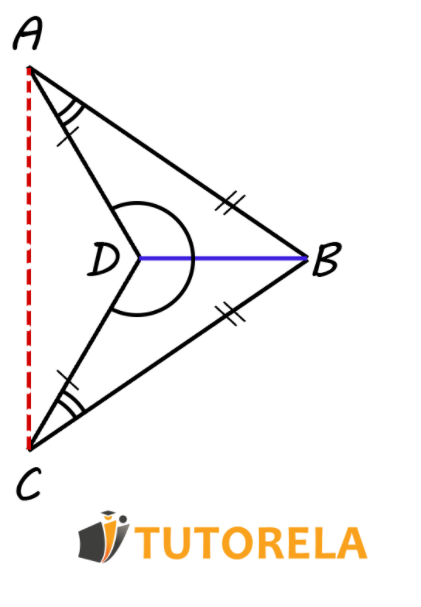
Demuestra que
Demostración:
Utilizaremos el criterio que hemos aprendido para probar que el triángulo y el son triángulos congruentes.
Responderemos que el lado es común a ambos triángulos (arista)
Así mismo se muestra que: (ángulo)
y que: (arista)
Por consiguiente, deduciremos que según el criterio de congruencia Lado, Ángulo, Lado (LAL).
Es primordial prestar atención y escribir el orden correcto de los vértices.
Luego de ver que los triángulos son congruentes podremos concluir que (Ángulos correspondientes en triángulos congruentes).
QED
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Criterio de congruencia: Ángulo, Lado, Ángulo
Criterio de congruencia: Lado, Lado, Lado
Lado, lado y el ángulo opuesto al mayor de los dos lados
Modo de escritura de la demostración formal en geometría
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Ejercicios de criterio de congruencia Lado, Ángulo, Lado
Ejercicio 1
Dado: bisectriz
¿A cuál teorema de superposición pertenece?
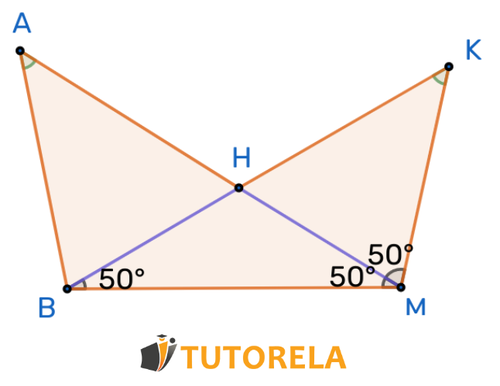
Solución
Lado común
Ángulo es igual al ángulo dado
Ángulo es igual a grados: dado
Ángulo es igual a grados: dado
Ángulo es igual a grados dado que: bisectriz de
Ángulo es igual al ángulo y por lo tanto igual a grados
Ángulo es igual al ángulo
Si los dos ángulos en el triángulo son iguales, entonces el tercero también es igual, los triángulos se superponen de acuerdo con el teorema de superposición (ángulo lado ángulo)
Respuesta
(ángulo lado ángulo)
En el dibujo dado:
AB=CD
\( ∢\text{BAC}=∢\text{DCA} \)
¿Según qué teorema, los triángulos Δ ABC ≅Δ CDA son congruentes?
\( \)
Ejercicio 2
Consigna
Las secciones y se cortan en el punto .
Dado: punto intersecta .
¿Según qué teorema de congruencia ?
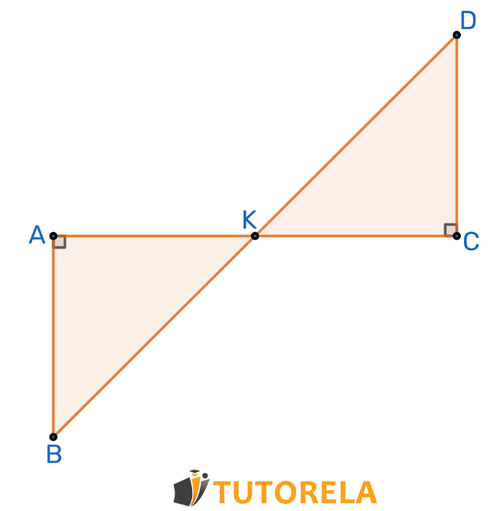
Solución
es perpendicular a
Una recta perpendicular crea un ángulo recto de grados, por lo tanto, el ángulo es igual a: grados
es perpendicular a
Una recta perpendicular crea un ángulo recto de grados, por lo tanto, el ángulo es igual a: grados
De esto se deduce que los ángulos
Dado el punto que intersecta a
Por lo tanto los triángulos superpuestos según el teorema (lado, ángulo, lado)
Respuesta
Superpuestos: (lado, ángulo, lado)
Ejercicio 3
Consigna
En la figura dada:
¿Según qué teorema de congruencia ?
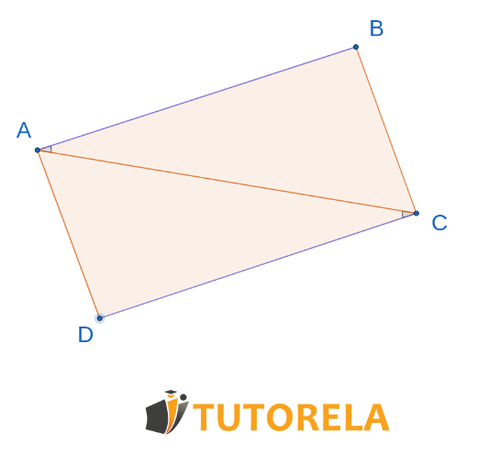
Solución
Dado que
Dado que los ángulos
Lado es un lado común
Los triángulos superpuestos según el teorema (lado, ángulo, lado)
Respuesta
Superpuestos según (lado, ángulo, lado)
En el dibujo dado:
AB=CD
\( ∢\text{BAC}=∢\text{DCA} \)
¿Según qué teorema, los triángulos Δ ABC ≅Δ CDA son congruentes?
\( \)
Ejercicio 4
Consigna
¿Los triángulos que aparecen en el dibujo son congruentes?
En caso afirmativo, explique de acuerdo con qué teorema de superposición
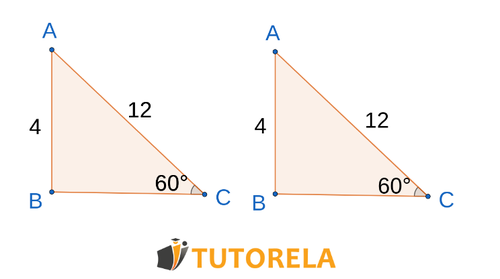
Solución
Ángulos
Los triángulos superpuestos según el teorema (lado, lado, ángulo)
Respuesta
Superpuestos según (lado, lado, ángulo)
Ejercicio 5
Consigna
¿Los triángulos y son congruentes?
Si es así, ¿de acuerdo con qué teorema de superposición?
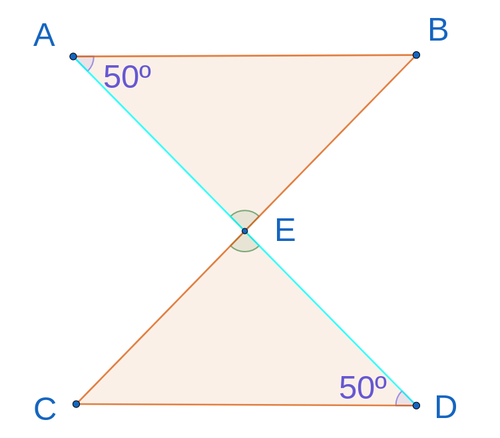
Solución
Dado que
ángulos
ángulo ángulos opuestos por el vértice
Los triángulos superpuestos según el teorema
Respuesta
Congruentes según (ángulo, lado, ángulo
En el dibujo dado:
AB=CD
\( ∢\text{BAC}=∢\text{DCA} \)
¿Según qué teorema, los triángulos Δ ABC ≅Δ CDA son congruentes?
\( \)
Ejercicio 6
Consigna
Dada la figura:
¿Según qué teorema se superponen los triángulos ?
Solución
Dado que
Dado que es paralela a
Ángulos ángulos alternos entre rectas paralelas iguales
lado común
Triángulos congruentes según teorema
Respuesta
Según teorema
Preguntas de repaso
¿Qué es un triángulo?
En geometría es considerada como una figura plana de tres lados, en donde la unión de cada lado, llamados vértices, se forman tres ángulos.
¿Qué son triángulos congruentes?
Si dos triángulos tienen lados y ángulos con la misma medida, entonces serán triángulos congruentes.
¿Qué criterios se pueden usar para determinar si dos triángulos son congruentes?
Existen cuatro criterios para poder determinar si dos triángulos son o no congruentes, los cuales son los siguientes:
- LAL- Lado, Ángulo, Lado.
- ALA- Ángulo, Lado, Ángulo.
- LLL- Lado, Lado, Lado.
- LLA- Lado, Lado, Ángulo.
¿Cuál es el criterio Lado, Ángulo, Lado?
Este criterio nos dice que dos triángulos son congruentes cuando dos de sus lados y el ángulo comprendido entre ellos correspondientes con el otro triángulo son iguales. Cabe mencionar que si el ángulo a analizar no es el comprendido entre estos dos lados no podemos utilizar este criterio.
¿Para qué tipo de triángulos podemos utilizar los criterios de congruencias?
Los criterios los podemos emplear en cualquier tipo de triángulos, ya sea un triángulo equilátero, un triángulo isósceles o escaleno.
En el dibujo dado:
AB=CD
\( ∢\text{BAC}=∢\text{DCA} \)
¿Según qué teorema, los triángulos Δ ABC ≅Δ CDA son congruentes?
\( \)
ejemplos con soluciones para Lado, ángulo, lado
Ejercicio #1
En el dibujo dado:
AB=CD
¿Según qué teorema, los triángulos Δ ABC ≅Δ CDA son congruentes?
Solución en video
Respuesta
Congruentes por L.A.L
- El Teorema de Pitágoras
- Triángulos congruentes
- Criterio de congruencia: Ángulo, Lado, Ángulo
- Criterio de congruencia: Lado, Lado, Lado
- Lado, lado y el ángulo opuesto al mayor de los dos lados
- Congruencia de triángulos rectángulos (en el contexto del Teorema de Pitágoras)
- Suma de los ángulos de un polígono
- Semejanza de triángulos y polígonos
- Semejanza de figuras geométricas
- Razón de semejanza
- Triángulos semejantes
- Criterios de semejanza de triángulos
- Rectángulos congruentes
- Suma de los ángulos internos de un polígono
- Ángulo exterior de un triángulo
- Suma de los ángulos externos de un polígono
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









