Criterio de congruencia: Ángulo, Lado, Ángulo

En este artículo estudiaremos el segundo criterio de congruencia:

Definición:

2 triángulos en los que 2 de sus ángulos y el lado comprendido entre ellos sean iguales son triángulos congruentes.

Atención: ¡Los dos ángulos deben ser contiguos al lado igual y correspondiente en ambos triángulos!

Para demostrar que 2 triángulos son congruentes podemos utilizar uno de los siguientes postulados:

• LAL - lado, ángulo, lado
• ALA - ángulo, lado, ángulo
• LLL- lado, lado, lado
• LLA- lado, lado, ángulo

Dados los triángulos $Δ ABC$  y $Δ DEF$ de modo que:
$\sphericalangle A=\sphericalangle D$
$AB = DE$
$\sphericalangle B=\sphericalangle E$

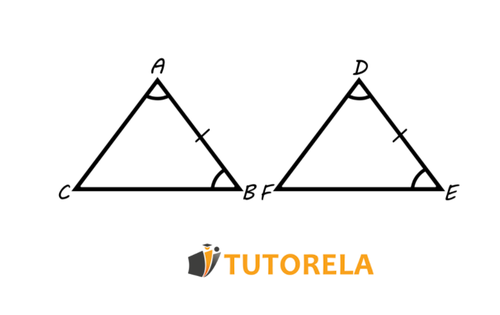
De esto se deduce que los triángulos $Δ ABC$ y $Δ DEF$ son congruentes, por lo tanto, escribiremos:

$Δ DEF ≅ Δ ABC$ según el criterio de congruencia: Ángulo, Lado, Ángulo (ALA)

Por consiguiente, deduciremos que:

$BC = EF$

$AC = DF$

ya que éstos son lados correspondientes e iguales en triángulos congruentes.

Entonces, también deduciremos que:

\\sphericalangle C=\sphericalangle F\)

ya que éstos son ángulos correspondientes e iguales en triángulos congruentes.

Dadas dos rectas paralelas. Entre ellas pasa la recta $AC$ y la recta $BD$ de tal modo que se cruzan en el punto $O$. Asimismo, se nos hace saber que $AO = OC$

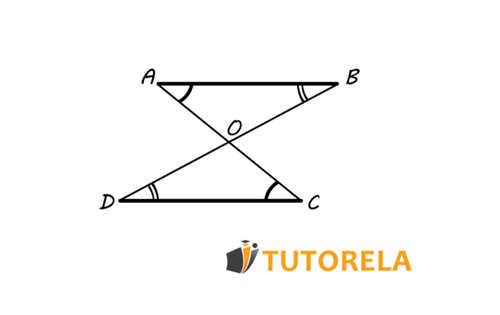
Demuestra que $AB = DC$

Demostración:
Primero debemos mostrar que los triángulos $Δ ABO$ y $Δ DOC$ son congruentes. Nos basaremos en el criterio anterior.

Prestemos atención a que \(\sphericalangle AOB = \sphericalangle COD\) (Por ser ángulos opuestos por el vértice)

Dado que $AE = EC$ (Lado)

Recordemos que las dos rectas dadas son rectas paralelas.

Por lo tanto, $​​\sphericalangle OAB=\sphericalangle OCD$ ya que son ángulos alternos entre rectas paralelas (ángulo).

Observaremos que ahora tenemos $2$ triángulos en los que $2$ de sus ángulos y el lado comprendido entre ellos son iguales.

Por consiguiente, los triángulos $Δ ABO$ y $Δ DOC$ son congruentes

y lo escribiremos $Δ ABO ≅ Δ DOC$según el criterio de congruencia Ángulo, Lado, Ángulo (ALA)

Por lo tanto, podremos deducir que $AB=DC$ (Lados correspondientes entre triángulos congruentes).

$QED$

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Criterio de congruencia: Lado, Ángulo, Lado

Criterio de congruencia: Lado, Lado, Lado

Lado, lado y el ángulo opuesto al mayor de los dos lados

Modo de escritura de la demostración formal en geometría

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.

Ejercicio 1

Consigna

Dado que el punto $K$ cruza a la mitad $AC$.

y también $∢A=∢C$

¿Según qué teorema de congruencia coinciden los triángulos $ΔAMK≅ΔCBK$?

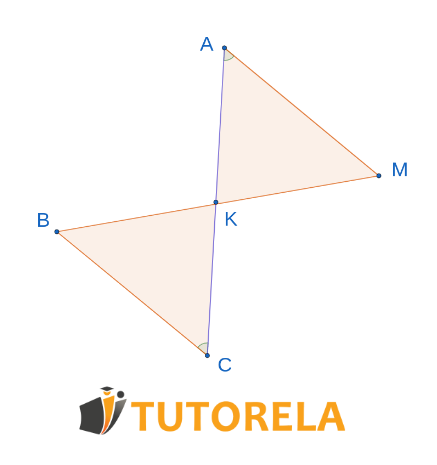
Solución

Dado que los ángulos $A=C$

$AK=KC$

Dado que el punto $K$ corta a $AC$

Ángulos $AKM=CKB$

Los ángulos opuestos por el vértice son iguales

Los triángulos son congruentes según el teorema $A.L.A$

Respuesta

$A.L.A$

Ejercicio 2

Consigna

Dado: el cuadrilátero $ABCD$ es un rectángulo.

¿Según qué teorema de congruencia coinciden los triángulos $ΔADO≅ΔCBO$?

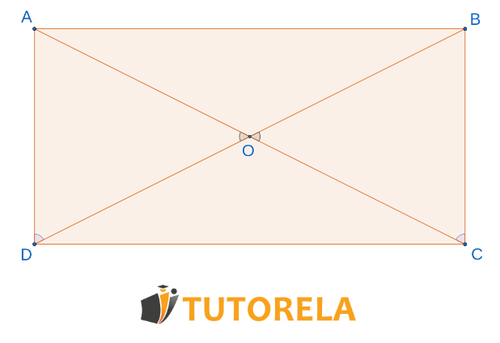
Solución

$BC=AD$

Dado que el cuadrilátero $ABCD$ es un rectángulo y en un rectángulo se tiene dos pares de lados paralelos e iguales

Ángulos $\sphericalangle BCO=\sphericalangle ADO$ Ángulos alternos entre líneas paralelas iguales.

Ángulos $O_1=O_2$

ángulos opuestos por el vértice son iguales

Entonces decimos que son triángulos congruentes según el teorema $L.A.A$

Respuesta

Según el teorema $L.A.A$

Ejercicio 3

Consigna

En la figura dada: $DE || AB$

y el punto $C$ corta a la mitad al segmento $BE$.

¿Según qué teorema de congruencia coinciden los triángulos?

$ΔABC≅ΔDEC$

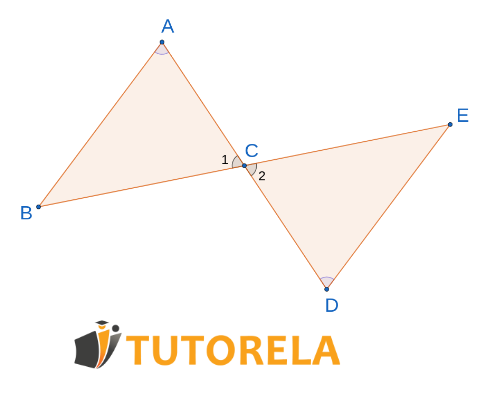
Solución

Dado que $DE$ es paralela a $AB$

Ángulos $D=A$

Los ángulos alternos son iguales entre rectas paralelas

$BC=CE$ El punto $C$ corta la recta $BE$

Ángulos $C_1=C_2$

Ángulos opuestos por el vértice

Triángulos congruentes según el teorema de superposición $L.A.A$

Respuesta

Superpuestos según $L.A.A$

Ejercicio 4

Consigna

Dado el triángulo $ΔEDC$ isósceles.

$∢ADE=∢BCE$

$AC=BD$

¿Según qué teorema de congruencia coinciden los triángulos?

$ΔADE≅ΔBCE$

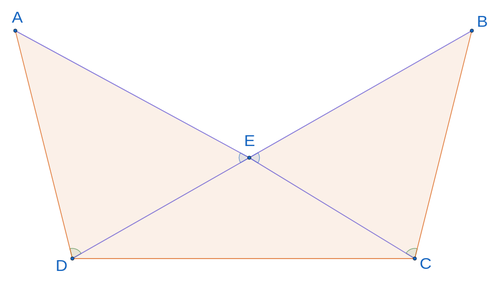
Solución

Triángulo $ΔEDC$ es un triángulo isósceles

$DE=EC$

En un triángulo isósceles, dos lados son iguales

Ángulos $D=C$ dado

ángulos $EDC=ECD$ los ángulos de la base del triángulo isósceles son iguales

ángulos $ADE=BCE$

$\sphericalangle D-\sphericalangle EDC=\sphericalangle C-\sphericalangle ECD$

Resta de ángulos

$\sphericalangle E_1=\sphericalangle E_2$

Triángulos congruentes según el teorema $A.L.A$

Respuesta

$A.L.A$

Ejercicio 5

Consigna

Dado: cuadrilátero $ABCD$ cuadrado.

Y dentro está encasillado el deltoide $KBPD$.

¿Según qué teorema de congruencia coinciden los triángulos $ΔBAK≅ΔBCP$?

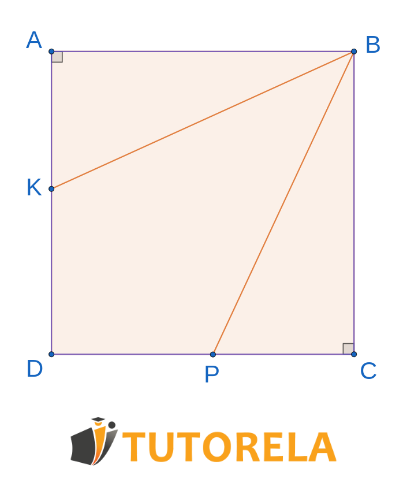
Solución

$ABCD$ es un cuadrado

$AB=BC$

En un cuadrado todos los lados son iguales

Dado que $KBPD$ es un deltoide

$BK=BP$

En el deltoide dos pares de lados adyacentes son iguales

$\sphericalangle C=\sphericalangle A$

Ángulos iguales en un cuadrado equivalen a $90°$ grados

$\sphericalangle BPC=\sphericalangle BKA$

Los ángulos del deltoide son iguales $\sphericalangle K=\sphericalangle P$

por lo tanto $180° -\sphericalangle K=180° -\sphericalangle P$

$\sphericalangle ABK=\sphericalangle PBC$

si dos ángulos son iguales entonces el tercero también es igual

Los triángulos iguales según $L.A.L$

Respuesta

$L.A.L$

¿Qué es un criterio en geometría?

En matemáticas un criterio es un juicio o una pauta que nos permite determinar ciertas características según sea el caso o tema a estudiar, en el caso de geometría nos permite juzgar ciertas características para figuras dadas.

¿Qué es el criterio de congruencia de triángulos?

Existen $4$ criterios de congruencia de triángulos, los cuales nos ayudan a determinar cuándo dos triángulos son congruentes, es decir, nos ayudan a determinar cuándo dos triángulos tienen las mismas dimensiones y ángulos correspondientes teniendo así la misma forma y medidas de lados sin importar la orientación que se encuentren dichos triángulos.

¿Cuál es el criterio AAL?

Decimos que dos triángulos son congruentes con el criterio AAL, cuando dos de sus ángulos y un lado no comprendido entre ellos correspondientes son congruentes.

¿Cuál es el criterio ángulo lado ángulo?

Este criterio me dice que dos triángulos son congruentes, cuando dos ángulos y el lado comprendido entre estos son congruentes.

¿Cómo saber el criterio de un triángulo?

Esto depende de los ángulos y lados correspondientes de ambos triángulos

Por ejemplo, dados dos triángulos:

Si tenemos los tres lados correspondientes de dos triángulos que son congruentes entonces estamos hablando del criterio LLL

Si se tiene que los dos ángulos y el lado comprendido entre los ángulos correspondientes son congruentes nos referimos al criterio ALA

Al observar que dos de sus ángulos y el lado no comprendido entre ellos son congruentes respectivamente entonces hablamos del criterio AAL

Y por último cuando dos pares de lados correspondientes y el ángulo comprendido entre estos lados son congruentes será el criterio de LAL.

De acuerdo a esto podremos determinar a qué criterio de congruencia nos estamos refiriendo y deducir si son o no triángulos congruentes.