Podemos calcular muy fácilmente la suma de los ángulos internos de un polígono según la siguiente fórmula:

Cuando: cantidad de aristas o lados del polígono
En realidad, la suma de todos los ángulos internos de un polígono depende de la cantidad de aristas que tenga.
Pasos por seguir para hallar la suma de los ángulos internos de un polígono:
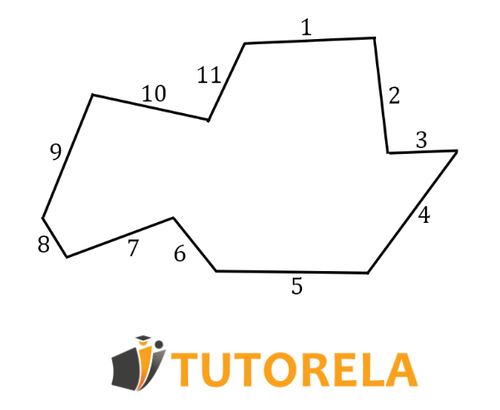
- Contemos cuántos lados tiene.
- Coloquémoslo en la fórmula y obtendremos la suma de los ángulos internos del polígono.
Pon atención:
En la fórmula hay paréntesis que requieren que primero realicemos las operaciones de restar (primero restaremos del número de aristas y sólo luego multiplicaremos por .)
Independientemente del polígono que tengas, cóncavo, convexo o regular, gracias a esta fórmula podrás hallar la suma de los ángulos internos de cualquier polígono.