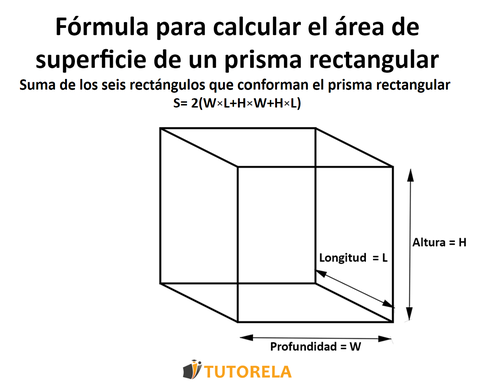
Los Prismas rectangulares están compuestos por rectángulos distintos. Cuando te enfrentes a un ejercicio o un examen en el que te piden calcular el área de superficie de un Prisma rectangular, utiliza la fórmula que te indicamos a continuación.
Cómo calcular el área de superficie de un prisma rectangular (ortoedro)
La fórmula: ¿cómo calcular el área de un prisma rectangular (ortoedro rectangular)?
S= área de superficie
¡Pruébate en área superficial del ortoedro!
Dado el ortoedro de la figura:
¿Cuál es la superficie del ortoedro?
Si cogemos como ejemplo un ortoedro con las siguientes características, su área de superficie se calculará tal y como exponemos a continuación:
Ancho = cm
Largo = cm
Altura = cm
Ahora, aplicamos la fórmula:
De este modo, al resolver el ejercicio obtendremos que el área de superficie del prisma rectangular (ortoedro) es cm².
Si este ejercicio le resulta fácil y está interesado en aprender a calcular la superficie de un prisma, puede aprenderlo en el siguiente artículo: Área de superficie de prismas triangulares.
Es importante recordar que en el examen el nombre de la forma puede variar de un ejercicio a otro.
por ejemplo: Prisma rectangular, Ortoedro y Cubo.
Por lo cual es importante recordar que se trata de una forma geométrica con caras, Aristas y Vértices.
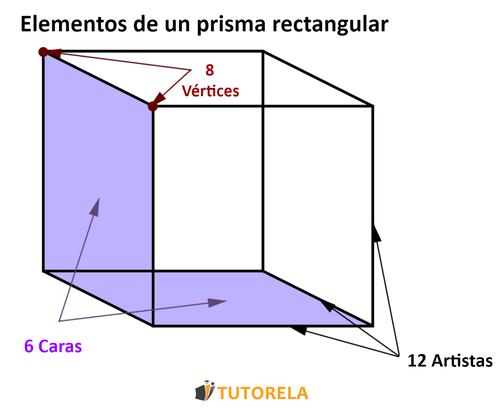
¿A qué conclusión llegamos?
A que el área de superficie de un prisma rectangular (ortoedro) es la suma de las áreas de todos los rectángulos que lo forman.
A lo largo de la primaria y de la secundaria, tendrás que hacer frente a ejercicios de todo tipo relacionados con el ámbito de la geometría. Por ello necesitarás saber cómo calcular el área de superficie de un prisma rectangular. Te presentamos la fórmula que te ayudará a hacerlo y te damos algunos consejos para interiorizar los materiales aprendidos de una forma mejor.
Si cogemos como ejemplo un prisma rectangular con las siguientes características, su área de superficie se calculará tal y como exponemos a continuación:
Ancho cm
Largo cm
Altura cm
El área de superficie del prisma rectangular es:
A que el área de superficie de un ortoedro es la suma de las áreas de todos los rectángulos que lo forman. Veámoslo ilustrado en la siguiente imagen:
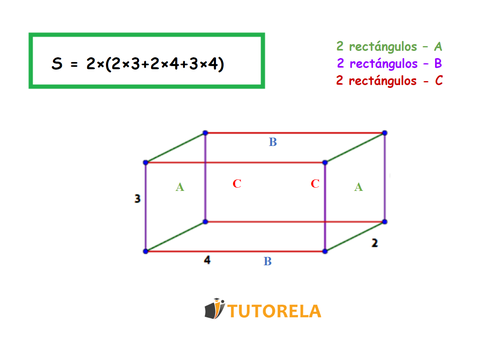
Respuesta:
De este modo, al resolver el ejercicio obtendremos que el área de superficie del prisma rectangular es cm².
¿A qué conclusión llegamos?
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Para una amplia gama de artículos de matemáticas visite el blog de Tutorela
Ejercicios para calcular la superficie de un prisma rectangular (ortoedro)
Ejercicio 1
Dados dos ortoedros
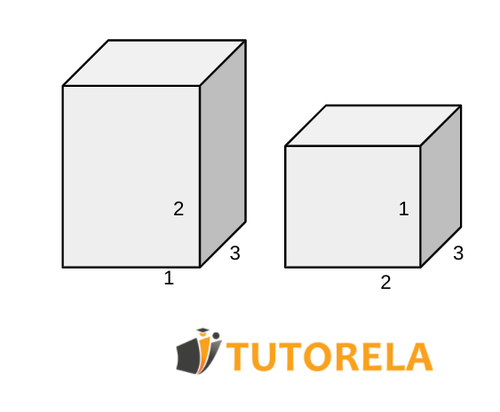
Tarea:
¿Acaso las superficies de los dos ortoedros son iguales o distintas?
Solución:
Observemos que los ortoedros son idénticos, simplemente están presentados de manera diferente.
Si damos la vuelta a uno de ellos, quedará claro que los cubos son idénticos.
Podemos verificar mediante el cálculo.
Ortoedro derecho :
Ortoedro izquierdo :
Respuesta:
Las superficies son iguales.
Dado el ortoedro de la figura:
¿Cuál es la superficie del ortoedro?
Dado el siguiente ortoedro
¿Cuál es la superficie?
Dado el siguiente ortoedro
¿Cuál es la superficie?
Ejercicio 2
Dada que la superficie del ortoedro es igual cm²
La altura del ortoedro es igual a cm y el ancho es cm.
Calcula el volumen del ortoedro
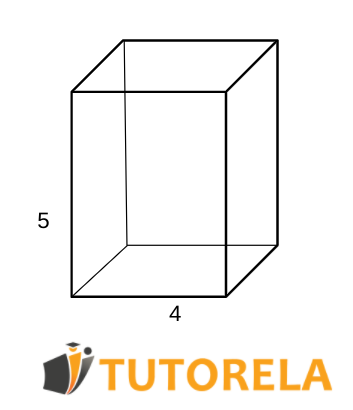
Tarea:
Calcular el volumen del ortoedro.
Solución:
Superficie = cm²
Largo = cm
Ancho = cm
Altura=
Reemplazamos la altura por
/ :dividimos en
El largo es igual a cm.
Lo reemplazamos en la fórmula del volumen:
Respuesta:
El volumen del ortoedro es igual a cm³
Ejercicio 3
Dado un cubo con la siguiente información:
Ancho cm
Largo cm
Altura cm
Cómo calcular el área de superficie del cubo
Respuesta:
El área de superficie del cubo es: cm²
¿Cuál es la superficie del ortoedro de la figura?
Dado un ortoedro cuyas dimensiones en el dibujo
¿Qué rectángulos forman el ortoedro?
Dado el ortoedro en el dibujo, ¿cuál es el despliegue apropiado?
Ejercicio 4
Dado un prisma rectangular con la siguiente información:
Ancho cm
Largo cm
Altura cm
Cómo calcular el área de superficie del prisma rectangular
Respuesta:
cm²
Ejercicio 5
Dado un prisma rectangular con la siguiente información:
Ancho cm
Largo cm
Altura cm
Cómo calcular el área de superficie del prisma rectangular
Respuesta:
El área de superficie del prisma rectangular es: cm²
Calcula la superficie del ortoedro mediante los datos del dibujo:
Dado el ortoedro cuya base cuadrada es de tamaño 25 cm²,
La altura del ortoedro es 3 cm,
¿Cuál es la superficie del ortoedro?
Dado el ortoedrocuya superficie es 102
Encuentra a X
Preguntas de repaso
¿Cómo se calcula el área total de un prisma rectangular?
Para calcular el área total de un prisma rectangular, se bebe de calcular las áreas de cada una de sus caras (6 caras) y posteriormente sumar el área de todas ellas para obtener el área total.
¿Cuál es la fórmula para sacar el área de un prisma?
Factorizando el
En donde:
Área de superficie
largo
ancho
altura
Dado el ortoedro de la figura:
Superficie 122 cm²
¿Cuál es el ancho del ortoedro?
Dado que la superficie del ortoedro es 147 cm²
¿Cuáles son las dimensiones del ortoedro que no aparecen en el dibujo?
Calcula el área de la superficie de la caja que aparece en el dibujo, presta atención a las unidades de medida:
¿Cómo calcular el área y volumen de un prisma rectangular?
El área de un prisma rectangular se calcula con la fórmula:
Mientras que el volumen se calcula con la siguiente fórmula:
Ejemplo
Sea el siguiente prisma rectangular con las siguientes medidas
Ancho
Largo
Altura
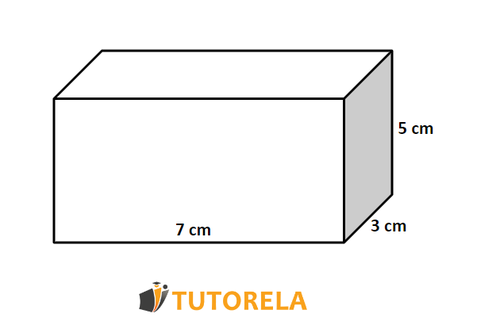
Vamos a calcular el área con la fórmula
Ahora calculamos el volumen
Resultado
¿Cómo se calcula el área de una caja rectangular?
Para calcular el área de una caja rectangular sumamos las áreas de sus seis caras, o usando la siguiente fórmula:
En donde:
Área de superficie
largo
ancho
altura
Dado un ortoedro cuya base es un cuadrado de tamaño 25 cm, su altura es igual a 3 cm
Halla la superficie del ortoedro.
El área de la superficie de un cubo es 24 cm², ¿cuál es la longitud del lado del cubo?
Dado el ortoedro de la figura:
¿Cuál es la superficie del ortoedro?
ejemplos con soluciones para Área superficial del ortoedro
Ejercicio #1
Dado el ortoedro de la figura:
¿Cuál es la superficie del ortoedro?
Solución en video
Solución Paso a Paso
Veamos qué rectángulos tenemos:
8*5
8*12
5*12
Recordemos la fórmula para la superficie de un ortoedro:
(largo X ancho + largo X altura + ancho X altura) 2
Ahora reemplazamos todo esto en el ejercicio:
(8*5+12*8+12*5)*2=
(40+60+96)*2=
196*2= 392
¡Esta es la solución!
Respuesta
392 cm²
Ejercicio #2
Dado el ortoedro de la figura:
¿Cuál es la superficie del ortoedro?
Solución en video
Solución Paso a Paso
Recuerda que la fórmula del área superficial de un ortoedro es:
(largo X ancho + largo X altura + ancho X altura) 2
Colocamos los datos conocidos en la fórmula:
2*(3*2+2*5+3*5)
2*(6+10+15)
2*31 = 62
Respuesta
62
Ejercicio #3
Dado el siguiente ortoedro
¿Cuál es la superficie?
Solución en video
Solución Paso a Paso
Primero, recordamos la fórmula para el área de superficie del ortoedro:
(ancho*largo + altura*ancho + altura*largo) *2
Como en el ortoedro, las caras opuestas son iguales entre sí, los datos existentes son suficientes para llegar a una solución.
Reemplazamos los datos en la fórmula:
(8*5+3*5+8*3) *2 =
(24+40+15) *2 =
79*2 =
158
Respuesta
158
Ejercicio #4
Dado el siguiente ortoedro
¿Cuál es la superficie?
Solución en video
Solución Paso a Paso
Identificamos que las caras son
3*3, 3*11, 11*3
Como las caras opuestas de un ortoedro son iguales, sabemos que por cada cara que encontramos hay otra cara, por lo tanto:
3*3, 3*11, 11*3
o
(3*3, 3*11, 11*3 ) *2
Para hallar el área de la superficie, tendremos que sumar todas estas áreas, por lo tanto:
(3*3+3*11+11*3 )*2
¡Y esta es en realidad la fórmula para el área de superficie!
Calculamos:
(9+33+33)*2
(75)*2
150
Respuesta
150
Ejercicio #5
Dado un ortoedro cuyas dimensiones en el dibujo
¿Qué rectángulos forman el ortoedro?
Solución en video
Solución Paso a Paso
Cada ortoedro, en realidad, esta compuesto de rectángulos, estos rectángulos son las caras del ortoedro.
Como sabemos que en un rectángulo las caras paralelas son iguales entre sí, podemos concluir que por cada cara encontrada habrá dos rectángulos.
Veamos primero la cara pintada de naranja,
Tiene ancho y alto, 5 y 3, entonces ya sabemos que son dos rectángulos de tamaño 5x6
Ahora veamos las caras de lado, también tienen una altura de 3, pero su ancho es de 6,
Y luego entendemos que hay dos rectángulos más de 3x6
Ahora veamos las caras superior e inferior, vemos que sus dimensiones son 5 y 6,
Por lo tanto, hay dos rectángulos más que tienen un tamaño de 5x6
Es decir, hay
2 rectángulos 5X6
2 rectángulos 3X5
2 rectángulos 6X3
Respuesta
2 Rectángulos 5X6
2 Rectángulos 3X5
2 Rectángulos 6X3
- La aplicación del teorema de Pitágoras en un ortoedro o cuboide
- Rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Área
- Perímetro
- Área del cilindro
- Volumen del cilindro
- Prisma rectangular (ortoedro)
- El cubo
- Cómo calcular el volumen de un prisma rectangular (ortoedro)
- Área lateral de un ortoedro
- Prisma triangular recto
- Las bases del prisma triangular recto
- Las caras laterales del prisma
- Aristas laterales de un prisma
- Altura del prisma
- El volumen del prisma
- Área de superficie de prismas triangulares
- Áreas de Polígonos para 7º Grado
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









