Un cilindro debe distinguirse entre área de superficie total y área de superficie lateral .
Área del cilindro
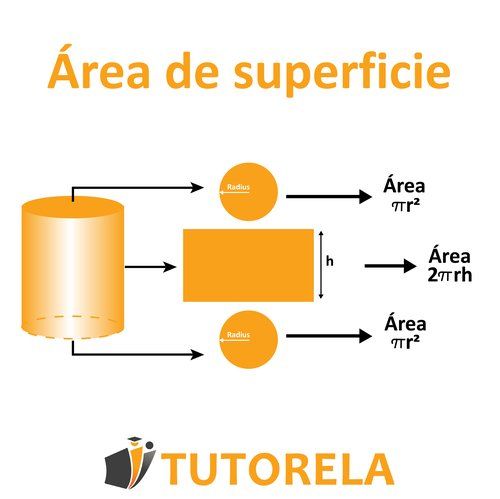
Cálculo del área de un cilindro
Área de la superficie
Área de superficie total es la suma de las áreas de las dos bases y la lateral (marcada en ). El área de la base es Y para obtener el área de las dos bases multiplicamos por , es decir, .
Para calcular el área lateral, volvemos a la forma rebanada. El ancho delrectángulo es Mientras que la longitud del rectángulo (lo denotamos por ) es igual a la circunferencia del círculo. La circunferencia del círculo se calcula mediante la fórmula. .
De esto obtenemos que el área lateral es el área del rectángulo rebanado, y debemos multiplicar el largo del rectángulo por el ancho del rectángulo.
El área del rectángulo resultante es .
Para obtener el área de la superficie total, sumaremos el área de las dos bases y el área lateral. Eliminaremos un factor común fuera de los paréntesis. Y obtenemos la siguiente fórmula:
Área de la superficie lateral
El área de la superficie lateral es solo la superficie lateral, sin las bases (marcadas en ). Es decir, nos referimos al área del rectángulo rebanado, que ya hemos calculado para el área total de la superficie.
La fórmula es:
Ejemplos y práctica del cilindro
Ejercicio N°1
Dado el cilindro que aparece en la figura.
Dependiendo de los datos, se debe encontrar el área de superficie lateral y el área de superficie total.

Tarea:
¿Cuál es el Área total de la superficie del cilindro: ?
Solución:
De la figura se puede observar que el radio de las bases es igual a cm, y la altura del cilindro es igual a cm.
Ahora solo queda colocar en las fórmulas que hemos aprendido.
Área de la superficie lateral
Área total de la superficie del cilindro:
Respuesta:
La superficie lateral es de cm², la superficie total es de cm².
Si este artículo te interesa, te pueden interesar los siguientes artículos:
Las bases del prisma triangular recto
Las caras laterales del prisma
Aristas laterales de un prisma
Área de superficie de prismas triangulares
En el blog de Tutorela encontrarás una gran variedad de artículos de matemáticas
- Elementos de la circunferencia
- Círculo
- Área de un circulo
- Distancia de la cuerda al centro del círculo
- Cuerdas en un círculo
- Ángulo central en un círculo
- Arcos en un círculo
- Perpendicular a la cuerda desde el centro del círculo
- Ángulo inscrito en un círculo
- Tangente de un círculo
- Perímetro de un circulo
- ¿Cómo se calcula el radio mediante su circunferencia?
- Volumen del cilindro
- Prisma rectangular (ortoedro)
- El cubo
- Cómo calcular el área de superficie de un prisma rectangular (ortoedro)
- Cómo calcular el volumen de un prisma rectangular (ortoedro)
- Área lateral de un ortoedro
- Prisma triangular recto
- Las bases del prisma triangular recto
- Las caras laterales del prisma
- Aristas laterales de un prisma
- Altura del prisma
- El volumen del prisma
- Área de superficie de prismas triangulares
- Componentes del Circuito
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones








