Los rectángulos congruentes son aquellos que tienen la misma área y el mismo perímetro.
Veamos un ejercicio a modo de ejemplo:
Dados los rectángulos y , tal y como se describen en el siguiente esquema:
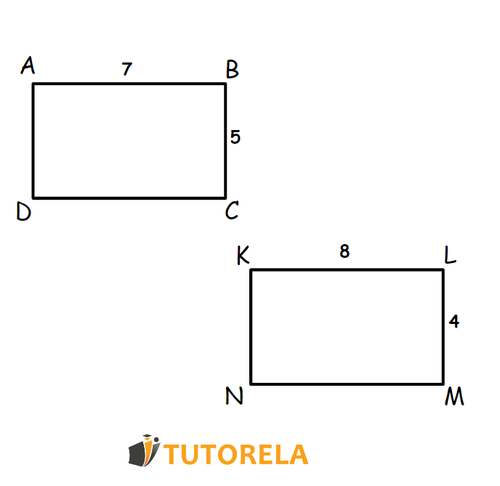
Observa los datos que aparecen en el esquema y determina si se trata de rectángulos congruentes.
En el primer rectángulo vemos lo siguiente:
Es decir, el perímetro equivale a y el área, a .
En el segundo rectángulo vemos lo siguiente:
Es decir, el perímetro equivale a y el área, a .
Los dos rectángulos tienen el mismo perímetro, pero su área es distinta.
Por lo tanto, no son congruentes.









