Un ángulo inscrito en un círculo es un ángulo cuyo vértice está en la parte superior del círculo (en la circunferencia del círculo) y cuyos extremos son cuerdas en un círculo.
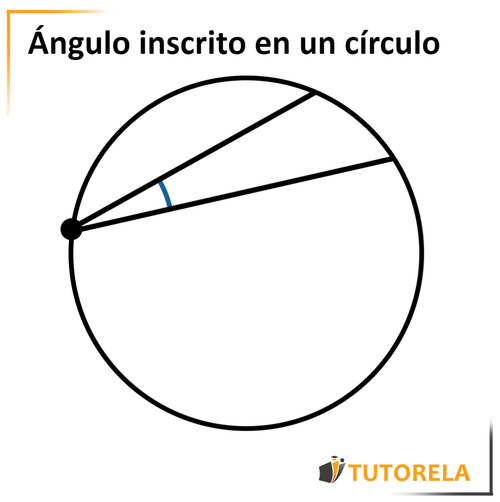
¿Dónde se encuentra un punto cuya distancia al centro del círculo es menor?
Estamos aquí para definir para ti cuál es el ángulo inscrito en una círculo. Además para darte consejos para recordar su definición y características de la manera más lógica.
Antes de hablar sobre el ángulo inscrito en el círculo, tomemos un momento para mirar su nombre - ángulo inscrito.
Su nombre, nos da a entender que tiene una conexión con la circunferencia y efectivamente así es.
Ahora, podemos pasar a la definición de un ángulo inscrito y se nos quedará en la mente gracias a la lógica.
¿Qué es el ángulo inscrito en un círculo?
El ángulo inscrito en un círculo es un ángulo cuyo vértice está en la parte superior del círculo: en la circunferencia del círculo y sus extremos son cuerdas en el círculo.
Veámoslo en la figura:
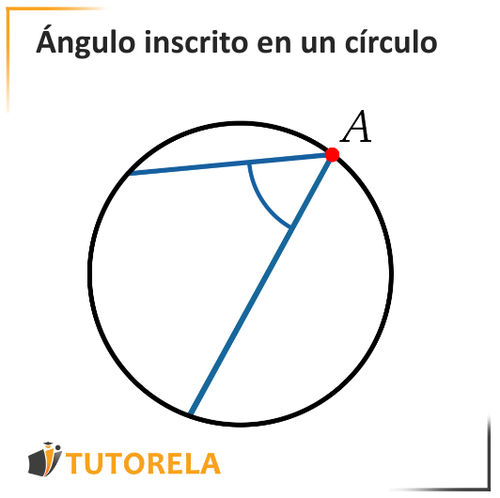
Tenemos un círculo frente a nosotros.
Mencionamos que un ángulo inscrito es un ángulo cuyo vértice está sobre el círculo, es decir, sobre la circunferencia.
y cuyos extremos son cuerdas en un círculo.
Por lo tanto, si traza dos cuerdas cualesquiera en un círculo, se encontrarán en el mismo punto de la circunferencia - Sobre el círculo mismo, crearemos un ángulo.
El ángulo que se formará, será un ángulo inscrito en el círculo.
Marcaremos A en algún punto del círculo y dos cuerdas dentro del círculo que se encuentran en el punto .
Ahora que sabemos qué es un ángulo inscrito en un círculo y podemos identificarlo fácilmente,
debemos conocer algunos teoremas y propiedades importantes de un ángulo inscrito en un círculo.
¿Comenzamos?
Los ángulos inscritos iguales
¿Cuándo podemos determinar que los ángulos inscritos un círculo son iguales?
Es decir, si hay alguna cuerda en la que inclinan ángulos inscritos del mismo lado, serán iguales.
Veamos esto en la figura:
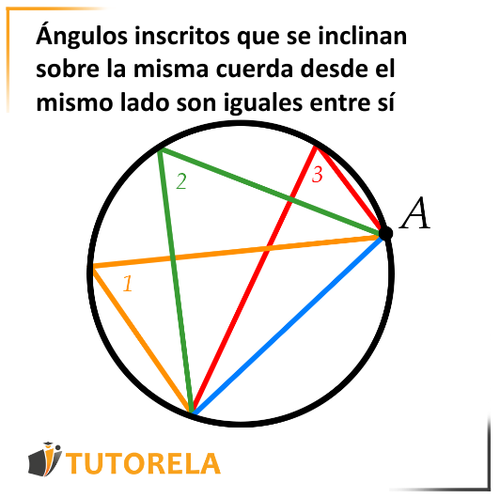
Aquí hay un círculo y una cuerda .
Podemos ver que los ángulos 1,2,3
se inclinan en la cuerda AB del mismo lado y por lo tanto son iguales.
Ejemplo de ángulos inclinados sobre la misma cuerda pero no del mismo lado:
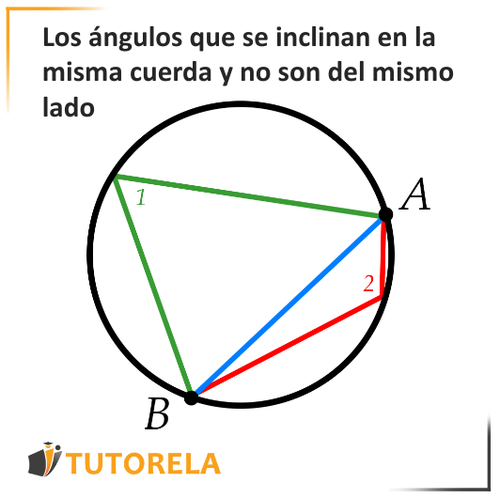
Podemos ver que los ángulos 1 y 2 sí se inclinan sobre la misma cuerda pero no del mismo lado y por lo tanto no podemos determinar que son iguales.
Un punto cuya distancia desde el centro del círculo es _______ que el radio, está fuera del círculo.
¿En cuál de los círculos se dibuja el radio del segmento?
¿En cuál de los círculos el segmento trazado es el radio?
Es decir, si nos dan que hay ángulos inscritos iguales, podemos determinar que las cuerdas y los arcos sobre los que se inclinan también son iguales.
Veamos esto en la figura:
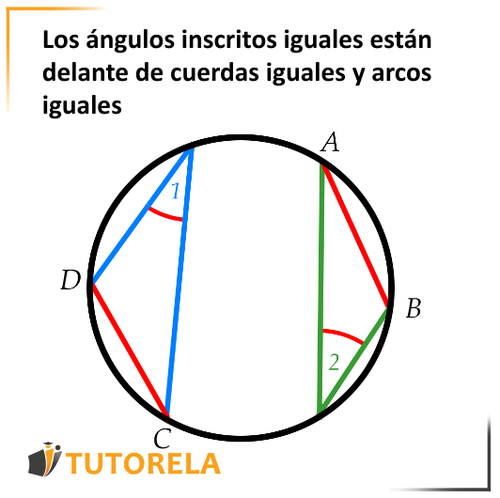
Ante nosotros hay un círculo
si se nos da que:
Entonces podemos determinar que:
y también
Es decir, si nos dan arcos iguales en un círculo, podemos determinar que los ángulos inscritos frente a ellos son iguales.
Veamos esto en la figura:
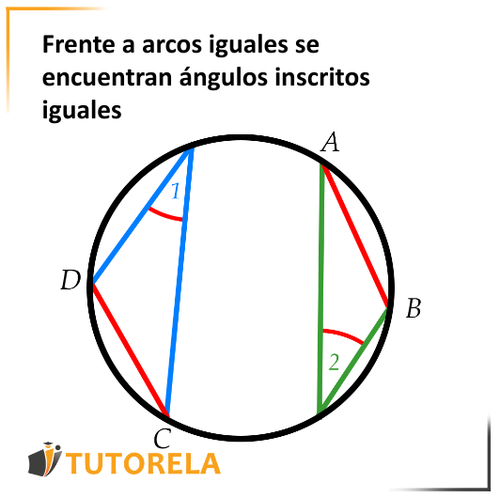
Ante nosotros hay un círculo.
Si nos dan que:
entonces
Ahora estudiaremos la relación entre un ángulo inscrito en un círculo y un ángulo central en un círculo.
Recuerda que un ángulo central en un círculo es un ángulo cuyo vértice está en el centro del círculo y cuyos extremos son radios en el círculo.
Como aquí:
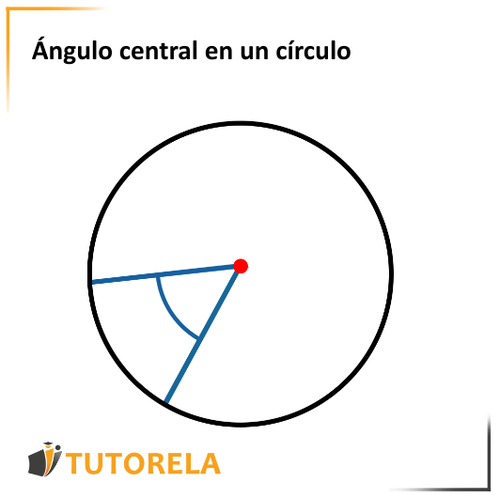
¿En cuál de los círculos está el punto marcado en el círculo y no sobre la circunferencia?
Calcula la longitud del arco pintado en rojo.
Dada la circunferencia igual a 24.
Calcula la longitud del arco pintado en rojo. Sabiendo que la circunferencia es 12.
En un círculo, el ángulo inscrito será la mitad del ángulo central que se inclina sobre el mismo arco.
Es decir:
Si en el círculo identificamos un ángulo central y un ángulo inscrito que se inclinan sobre el mismo arco, podemos decir que como se inclinan sobre el mismo arco, el ángulo inscrito será igual a la mitad del ángulo central .
Veamos esto en la figura:
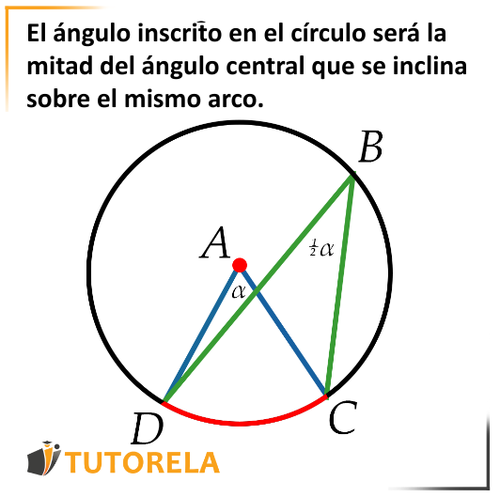
Recuerda, el diámetro es el radio más grande en un círculo: una línea que conecta 2 puntos en la parte superior del círculo y pasa por el centro del círculo.
¿Cuál es la relación entre este y el ángulo circunferencial? Excelente que preguntaste.
Un ángulo inscrito que se inclina sobre un diámetro igual a grados.
De la misma manera, podemos decir que si cualquier ángulo inscrito en un círculo es igual a grados, se inclina en un diámetro.
Veamos esto en la figura:
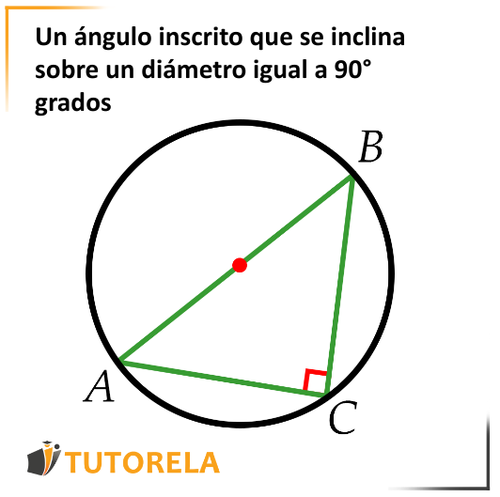
Si el diámetro
entonces
de la misma manera, si
entonces
es el diámetro.
Calcula la longitud del arco pintado en rojo. Sabiendo que la circunferencia es 36.
Calcula la longitud del arco pintado en rojo. Sabiendo que la circunferencia es 12.
Calcula la longitud del arco pintado en rojo. Sabiendo que la circunferencia es 6.
¿Recuerdas que hablamos sobre el hecho de que los ángulos inscritos inclinados sobre la misma cuerda en un lado son iguales?
Ahora, estamos hablando de los ángulos inscritos inclinados sobre la misma cuerda pero en sus dos lados diferentes. Los dos ángulos juntos suman grados.
Veamos esto en la figura:
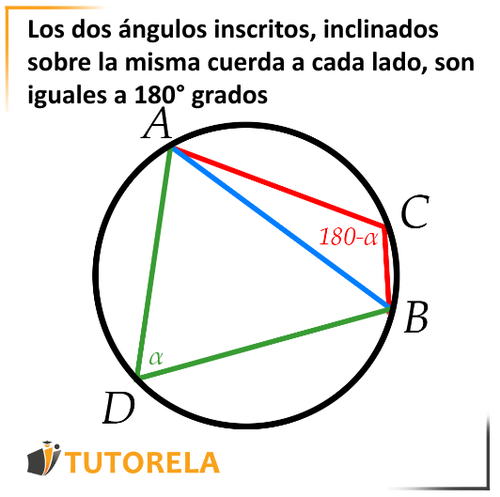
Frente a nosotros hay un círculo y una cuerda
Los ángulos y
son ángulos inscritos que se inclinan sobre la misma cuerda en sus dos lados diferentes y por lo tanto su suma será .
Si este artículo te interesa, también te pueden interesar los siguientes artículos:
En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Dado un círculo cuya ecuación es:
El punto O es su centro y está en el segundo cuadrante ()
Usa el método de completar el cuadrado para encontrar el centro del círculo y su radio en términos de .
Recordemos que la ecuación de un círculo con su centro en y su radio es:
Ahora, veamos la ecuación del círculo dado:
Intentaremos reorganizar esta ecuación para que coincida con la ecuación del círculo, o en otras palabras, nos aseguraremos de que en el lado izquierdo esté la suma de dos expresiones binomiales al cuadrado, una para x y otra para y.
Haremos esto utilizando el método de "completar el cuadrado":
Recordemos la fórmula corta para elevar un binomio al cuadrado:
Trataremos por separado la parte de la ecuación relacionada con x en la ecuación (subrayada):
Aislaremos estos dos términos de la ecuación y los trataremos por separado.
Presentaremos estos términos en una forma similar a la forma de los dos primeros términos en la fórmula abreviada (elegiremos la forma de resta de la fórmula del binomio al cuadrado ya que el término en la primera potencia con el que estamos tratando es, que tiene un signo negativo):
Observa que en comparación con la fórmula corta (que está en el lado derecho de la flecha azul en el cálculo anterior), en realidad estamos haciendo la comparación:
Por lo tanto, si queremos obtener una forma de binomio al cuadrado de estos dos términos (subrayados en el cálculo), necesitaremos agregar el término, pero no queremos cambiar el valor de la expresión, y por lo tanto también restaremos este término de la expresión.
Es decir, agregaremos y restaremos el término (o expresión) que necesitamos para "completar" la forma del binomio al cuadrado,
En el siguiente cálculo, el "truco" está resaltado (dos líneas bajo el término que agregamos y restamos de la expresión),
A continuación, pondremos la expresión en la forma de binomio al cuadrado la expresión apropiada (resaltada con colores) y en la última etapa simplificaremos la expresión:
Resumamos los pasos que hemos dado hasta ahora para la expresión con x.
Haremos esto dentro de la ecuación dada:
Continuaremos y haremos lo mismo para las expresiones con y en la ecuación resultante:
(Ahora elegiremos la forma de adición de la fórmula del binomio al cuadrado ya que el término en la primera potencia con el que estamos tratando tiene un signo positivo)
En el último paso, movemos los números libres al segundo lado y combinamos términos semejantes.
Ahora que la ecuación del círculo dado está en la forma de la ecuación general del círculo mencionada anteriormente, podemos extraer fácilmente tanto el centro del círculo dado como su radio:
En el último paso, nos aseguramos de obtener la forma exacta de la ecuación general del círculo, es decir, donde solo se realiza resta dentro de las expresiones al cuadrado (enfatizado con una flecha)
Por lo tanto, podemos concluir que el centro del círculo está en: y extraer el radio del círculo resolviendo una ecuación simple:
Recuerda que el radio del círculo, por su definición, es la distancia entre cualquier punto del diámetro y el centro del círculo. Como es positivo, debemos descalificar una de las opciones que obtuvimos para el radio.
Para hacer esto, utilizaremos la información restante que no hemos usado aún, que es que el centro del círculo dado O está en el segundo cuadrante.
Es decir:
(O en palabras: el valor de x del centro del círculo es negativo y el valor de y del centro del círculo es positivo)
Por lo tanto, debe ser cierto que:
Concluimos que y como el radio del círculo es positivo, concluimos que necesariamente:
Resumamos:
Por lo tanto, la respuesta correcta es la opción d.
¿En cuál de los círculos el segmento trazado es el radio?
¿En cuál de los círculos está el punto marcado en el círculo y no sobre la circunferencia?
Calcula la longitud del arco pintado en rojo.
Dada la circunferencia igual a 24.
Calcula la longitud del arco pintado en rojo. Sabiendo que la circunferencia es 12.
2
Calcula el área de la sección pintada de rojo. Dado que el área del círculo es 12.
¿Cuántas veces mayor es la longitud del radio del círculo rojo que la longitud del radio del círculo azul?
¿Cuántas veces mayor es la longitud del radio del círculo rojo que la longitud del radio del círculo azul?