Pi

Pi es un valor matemático, aproximadamente igual a $3,14$. Esta es la aproximación comúnmente utilizada para los cálculos. 

Pi se simboliza por $π$.

Ejemplos de algunas expresiones matemáticas que incluyen $π$:

$P=2\times R\timesπ$

$S=π\times R\times R$

Si este artículo te interesa, también te pueden interesar los siguientes artículos:

• La circunferencia
• El centro de la circunferencia
• Círculo
• Radio
• Diámetro
• El perímetro de la circunferencia
• Área circular
• Arcos en un círculo
• Cuerdas en un círculo
• Ángulo central en un círculo
• Perpendicular a la cuerda desde el centro del círculo
• Ángulo inscrito en un círculo

En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas

¿Qué representa el número Pi?

¿Cuál es el valor del número Pi?

¿Cuáles son las características del número Pi?

¿Expresión del número "Pi" en fracción?

Consigna

Dado el deltoide $ABCD$ y el círculo cuyo centro $O$ se encuentra sobre la diagonal $BC$

El área del deltoide es $28\operatorname{cm}²$

$AD=4$

¿Cuál es el área del círculo?

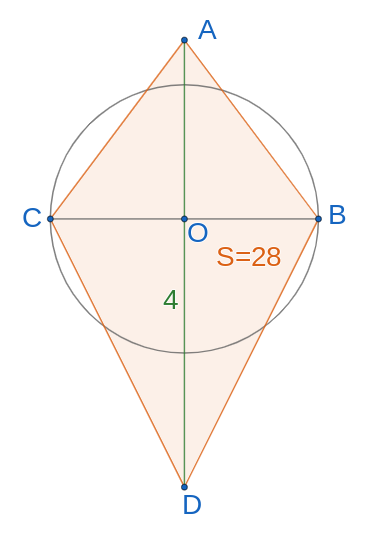
Solución

Área del deltoide $ABCD$

$28=\frac{AD\cdot CB}{2}=2CB$

Dividido por $2$

$14=CB$

El diámetro del círculo es $CB$

El diámetro multiplicado por la mitad es igual al radio

Reemplazamos en consecuencia

$\frac{1}{2}\cdot14=7$

$A=\pi r^2=\pi\cdot7^2$

$A=49\pi$

Respuesta

$49\pi$

Consigna

Dadas las partes del círculo que aparece en la figura (blancas)

Diámetro del círculo $11\operatorname{cm}$

¿Cuánto es el área de las partes juntas?

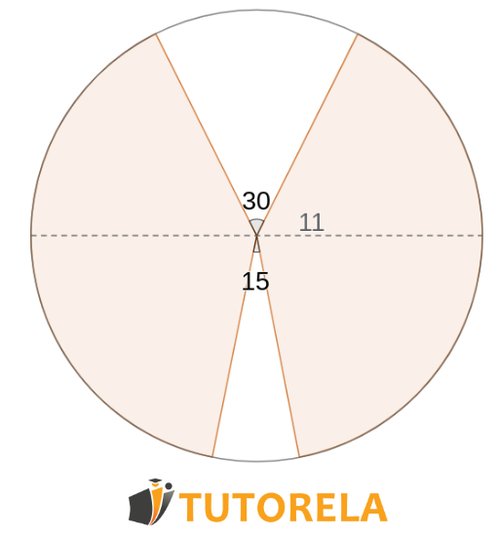
El área de las partes es como el área del círculo menos las dos secciones, una de las cuales se extiende por un ángulo de $30°$ y la otra por un ángulo de $15°$

De la misma manera podemos observar las partes así:

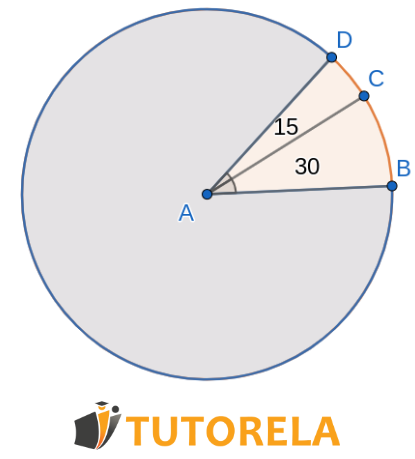
Entonces su área es el área del círculo menos el área de la sección extendida por un ángulo de $(45°)$

O es solo un área de corte que se extiende por $(360°)$ grados menos $(45°)$ grados, es decir,$(315°)$ grados

$A=\frac{315°}{360°}\cdot\pi\cdot(\frac{11}{2})^2=83.11$

Respuesta

$83.11\operatorname{cm}²$

Consigna

¿Cuál es el área de una porción de pizza que su diámetro es $45\operatorname{cm}$ luego de dividirse en $8$ porciones?

Solución

Pizza dividida por: $8$ porciones

Es decir que el área de una porción de pizza es $\frac{1}{8}$

$Apizza=\pi\cdot r²=\pi\cdot(\frac{diámetropizza}{2})²$

$\pi\cdot(\frac{45}{2})^2=506.25\pi$

$A=\frac{1}{8}\cdot506.25\pi$

$198.7\operatorname{cm}²$

Respuesta

$198.7\operatorname{cm}²$

Consigna

Dada la circunferencia que en su centro $O$

¿Es posible calcular su área?

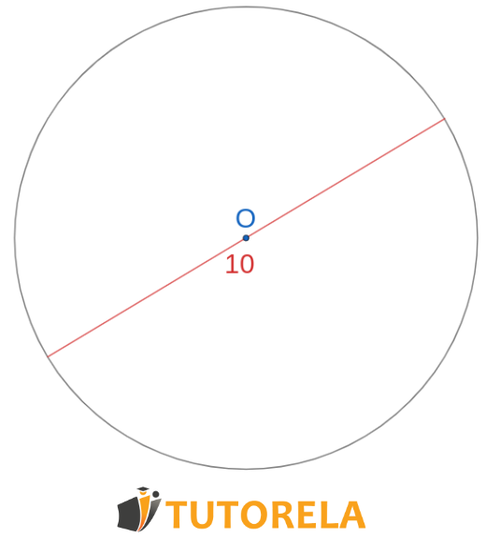
Solución

El centro de la circunferencia es $O$

Es decir, la recta dada es el diámetro.

Diámetro = Radio multiplicado por 2

$2r=10$

$r=5$

Usamos la fórmula de cálculo del área

$S=\pi r^2=$

$\pi5^2=25\pi$

Respuesta

Si, su área es $25\pi$

Consigna

Dado el círculo de la figura. $AB$ es la cuerda

¿Es posible calcular el área del círculo?

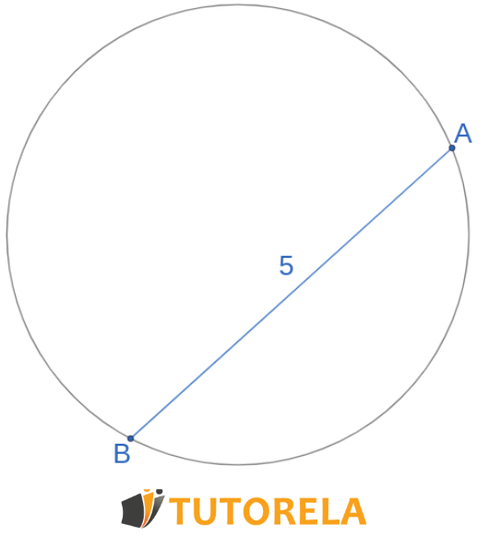
Solución

No sabemos nada sobre $AB$ aparte de que es una cuerda no se nos ha dado el diámetro o el radio, por lo tanto no es posible calcular el área

Respuesta

No es posible calcular el área

El número pi en pocas palabras es el número de veces que cabe el diámetro en toda la circunferencia, en este caso cabe $3.14159265358$, que es el valor de $\pi$.

Diferentes matemáticos estudiaron la relación que tenía el diámetro con la circunferencia o perímetro. Entonces estudiaron que el diámetro cabe $3.1415$ veces en toda la circunferencia aproximadamente, La manera de obtener el valor de pi es con la siguiente fórmula:

$\frac{\text{circunferencia}}{diámetro}=\pi$

El valor aproximado de pi es de $3.14159265358$, pero para utilizarlo solo bastan de dos o 4 decimales, es decir podemos tomar a $\pi=3.14$ o $\pi=3.1416$ si lo redondeamos.

El número pi tiene una infinidad de decimales y es por eso que se considera un número irracional, pero entre los estudios de pi, se suelen usar o conocer de 10 a 15 decimales.