La razón de semejanza es la diferencia constante entre los lados correspondientes de las dos formas.
Es decir, si la razón de semejanza es , sabemos que cada lado del triángulo grande es veces más grande que el del pequeño triángulo.
Razón de semejanza
¿Qué es la razón de semejanza?
¿Cómo calculamos la razón de semejanza?
El cálculo de la razón de semejanza se divide en varios pasos que se deben realizar:
- Primero debemos saber que se trata de triángulos o polígonos semejantes.
- Debemos saber identificar los lados correspondientes en cada uno de los triángulos o polígonos.
- Necesitamos saber los tamaños de un par de lados iguales.
- Debemos dividir el tamaño de un lado por el tamaño del otro lado.
El resultado obtenido es en realidad la razón de semejanza.
¡Pruébate en razón de semejanza!
¿La razón de semejanza entre los tres triángulos es igual a uno?
Lo ejemplificaremos a través de un ejercicio.
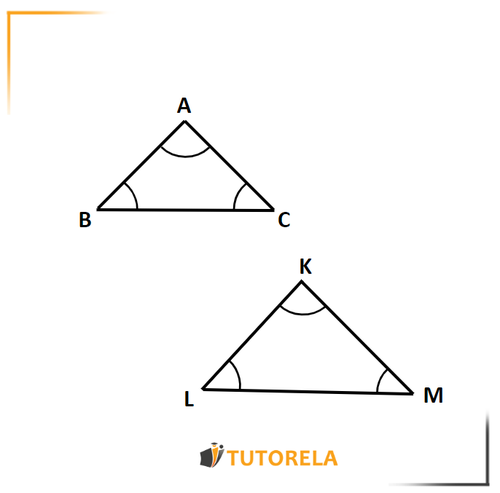
En el dibujo que tenemos ante nosotros hay dos triángulos semejantes a y .
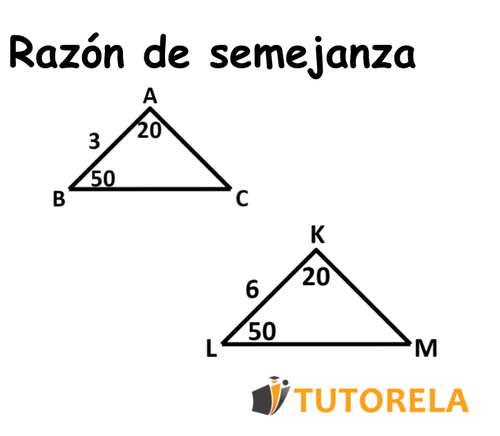
Se requiere que calculemos la razón de semejanza entre los dos triángulos.
Vamos a trabajar de acuerdo con los pasos descritos anteriormente.
El primer paso en realidad se ha completado - Se nos ha dado, porque estos son dos triángulos semejantes.
En el segundo paso, debemos identificar los lados correspondientes en cada uno de los dos triángulos. Observaremos el dibujo y veremos que los dos triángulos tienen ángulos. El ángulo es igual e igual al ángulo y el ángulo es igual al ángulo .
De esto se puede concluir que, en términos de ubicación, los lados y son lados correspondientes.
El tercer paso es bastante fácil, porque nos dan los tamaños de estos dos lados, ,
En el cuarto y último paso, realizaremos una sencilla operación de división de los tamaños de los lados correspondientes.
Obtenemos:
Obtenemos que la razón de semejanza de estos dos triángulos semejantes es igual a .
Si te interesa este artículo también te pueden interesar los siguientes artículos
- Semejanza de triángulos y polígonos
- Triángulos semejantes
- Triángulo
- Criterio de semejanza entre dos triángulos
- Semejanza de figuras geométricas
En la página web de Tutorela encontrarás una gran variedad de artículos de matemáticas
Ejercicios de razón de semejanza
Ejercicio 1
Consigna
Dado:
Elija la respuesta correcta
Solución
Según los dos triángulos son semejantes.
Respuesta
Respuestas
Dado que el los triángulos ABC y DEF son semejantes, ¿cuál es la razón de semejanza?
¿Según qué teorema los triángulos son congruentes en el dibujo? Completa la razón de semejanza
\( \frac{AB}{DF}=\frac{BC}{}=\frac{}{EF} \)
Dado que BC es paralela a DE
Completa:
\( \frac{AD}{}=\frac{AE}{AC} \)
Ejercicio 2
Consigna
Los triángulos semejantes:
Solución
Los triángulos son semejantes como resultado de la razón de similitud.
Respuesta
Ejercicio 3
Consigna
¿Cuál es la razón entre los lados de los triángulos y ?
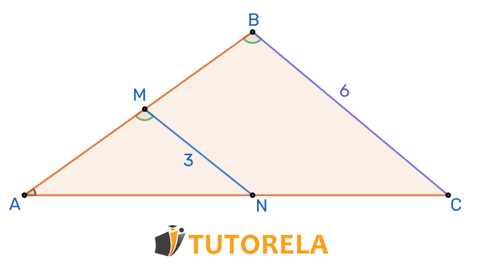
Solución
De la imaginación sale:
Respuesta
Ejercicio 4:
Consigna
Elija la respuesta correcta
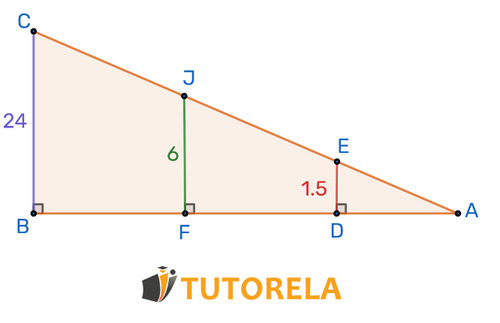
Solución
Razón de semejanza
Respuesta
¿Según cuál teorema la semejanza de los triángulos es congruente? ¿Cuál es la razón de semejanza?
Dado que los triángulos en el dibujo son semejantes, es decir, el triángulo DFE es semejante al triángulo ABC.
Halla a FE
Dado que los triángulos son semejantes, completa la razón de semejanza
\( \frac{AB}{}=\frac{}{EF}=\frac{AC}{} \)
Ejercicio 5
Consigna
Halla la razón de semejanza correspondiente a los triángulos y .
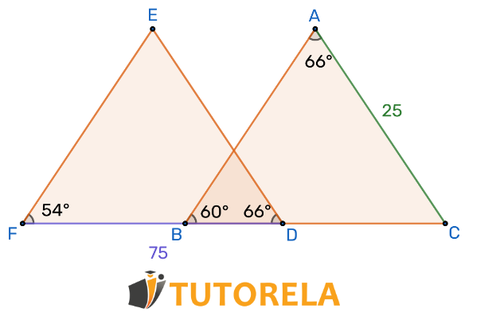
Solución
De esto se deduce que
Respuesta
Preguntas de repaso
¿Qué es la razón de semejanza?
Es el cociente de dividir los lados correspondientes de dos figuras.
¿Cómo sacar la razón de semejanza?
La razón de semejanza se saca dividiendo los lados correspondientes de dos figuras semejantes. Veamos un ejemplo:
Dado los siguientes triángulos semejantes
Calcular la razón de semejanza
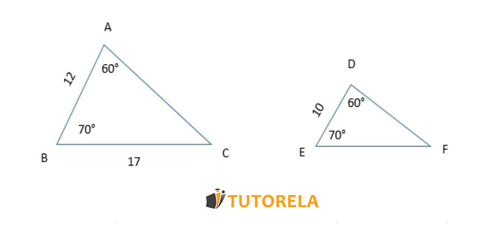
Dado que
Entonces debemos de ubicar cuales son los lados correspondientes, y de aquí deducimos que
Entonces los lados correspondientes son ,
Ahora para calcular la razón de semejanza hacemos el cociente de estos dos lados.
Por lo tanto la razón de semejanza es
¿Qué son dos triángulos semejantes?
Podemos decir que dos triángulos son semejantes cuando tienen la misma forma aunque tengan diferentes tamaños, para eso deben de cumplir con algunos de los siguientes criterios de semejanzas:
- Lado-Lado-Lado (LLL): Si la razón de sus tres pares de lados correspondientes es la misma entonces dos triángulos son semejantes.
- Lado-Ángulo- Lado (LAL): Dos triángulos son semejantes si la razón de dos pares de lados correspondientes es la misma y el ángulo que está comprendido entre estos dos pares en el mismo, entonces serán triángulos semejantes.
- Ángulo-Ángulo (AA): Para que dos triángulos sean semejantes por este criterio, dos de sus ángulos respectivos deberán medir lo mismo y por ende el tercer ángulo también debe de tener la misma medida que el correspondiente a ese ángulo. Es decir, sus tres ángulos correspondientes miden lo mismo.
¿Qué son figuras congruentes?
A diferencia de figuras semejantes que no necesariamente deben de medir lo mismo, dos figuras son congruentes cuando tienen la misma forma pero sus lados correspondientes miden lo mismo.
¿Cuál es la razón de semejanza de dos rectángulos?
Al igual que los triángulos semejantes, para poder calcular la razón de semejanza debemos de calcular el cociente de los lados correspondientes. Veamos un ejemplo:
Dado los siguientes rectángulos semejantes
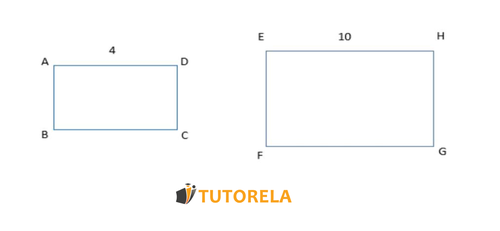
Calcular la razón de semejanza
Dado que son rectángulos semejantes y por ser cuadriláteros tienen ángulos rectos, entonces podemos deducir sus lados correspondientes:
Unos de sus lados correspondientes son ,, entonces podemos calcular la razón de semejanza.
Por lo tanto la razón de semejanza es
Cuál es la razón de semejanza \( \frac{BC}{BE} \)
Dado:
\( ΔACB∼ΔBED \)
Elija la respuesta correcta
Halla los triángulos semejantes en el dibujo y escribe la razón de semejanza.
ejemplos con soluciones para Razón de semejanza
Ejercicio #1
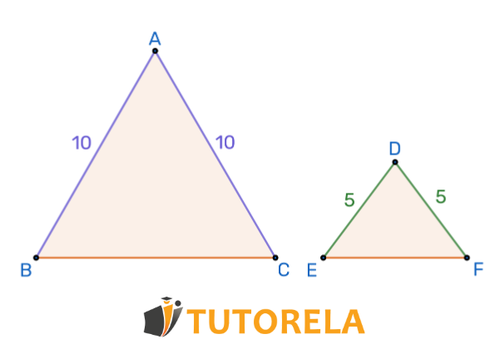
¿La razón de semejanza entre los tres triángulos es igual a uno?
Solución Paso a Paso
Para responder a la pregunta, primero debemos entender qué es la "razón de semejanza".
En triángulos semejantes, la razón entre los lados es constante.
En la consigna, no tenemos datos de ninguno de los lados.
Sin embargo, una razón de semejanza de 1 significa que los lados son exactamente del mismo tamaño.
Es decir, los triángulos no solo son semejantes sino también congruentes.
En el dibujo, puedes observar claramente que los triángulos son de diferentes tamaños y, por lo tanto, claramente la relación de similitud entre ellos no es 1.
Respuesta
No verdadero
Ejercicio #2
Dado:
Elija la respuesta correcta
Solución en video
Solución Paso a Paso
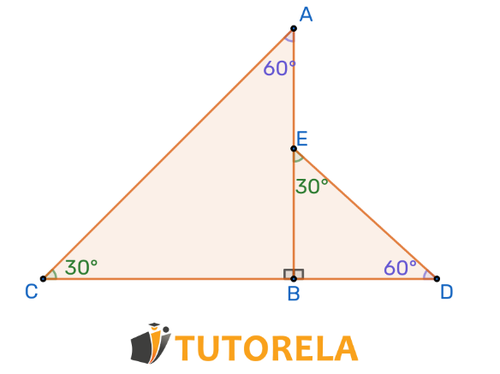
Primero observemos los ángulos C y E que son iguales a 30 grados:
El ángulo C es el lado opuesto de AB y el ángulo E es el lado opuesto de BD.
Ahora observemos el ángulo B que es igual a 90 grados en ambos triángulos:
En el triángulo ABC el lado opuesto es AC y en el triángulo EBD el lado opuesto es ED.
Observemos los ángulos A y D que son iguales a 60 grados:
El ángulo A es el lado opuesto de CB, el ángulo D es el lado opuesto de EB
Es decir, a partir de esto se puede argumentar que:
Y también:
Respuesta
Respuestas a + b
Ejercicio #3
¿Cuál es la razón entre los lados de los triángulos ΔABC y ΔMNA?
Solución en video
Solución Paso a Paso
De los datos del dibujo parece que el ángulo M es igual al ángulo B
También el ángulo A es un ángulo compartido por ambos triángulos ABC y AMN
Es decir, los triángulos ABC y AMN son semejantes respectivamente según el teorema del ángulo - ángulo.
Según las letras los lados que son iguales entre sí son:
Ahora podemos calcular la razón entre los lados de los triángulos dados:
Respuesta
Ejercicio #4
En la imagen aparecen un par de triángulos semejantes y un triángulo que no es semejante a los demás y escriba su razón de semejanza.
Solución Paso a Paso
El triángulo a y el triángulo b son semejantes según el teorema L.L.L (lado lado lado)
Y la relación entre los lados es idéntica:
Es decir, la razón entre ellos es 1:3.
Respuesta
y , razón de semejanza
Ejercicio #5
Dados dos triángulos semejantes, halla el perímetro del triángulo más grande.
Solución en video
Solución Paso a Paso
Calculamos el perímetro del triángulo pequeño (superior):
Por lo tanto, de la semejanza se entiende que la razón entre los lados del triángulo es igual a la razón entre los perímetros de los triángulos.
Identificaremos el perímetro del triángulo grande con una X:
Respuesta
36
- Triángulos congruentes
- Criterio de congruencia: Lado, Ángulo, Lado
- Criterio de congruencia: Ángulo, Lado, Ángulo
- Criterio de congruencia: Lado, Lado, Lado
- Lado, lado y el ángulo opuesto al mayor de los dos lados
- Suma de los ángulos de un polígono
- Semejanza de triángulos y polígonos
- Semejanza de figuras geométricas
- Triángulos semejantes
- Criterios de semejanza de triángulos
- Rectángulos congruentes
- Suma de los ángulos internos de un polígono
- Ángulo exterior de un triángulo
- Suma de los ángulos externos de un polígono
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









