Suma de fracciones

En este artículo aprenderás las maneras más fáciles para la adición de fracciones, esto te permitirá sumar todo tipo de fracciones sin ningún inconveniente.
¿Empezamos?

El primer paso para resolver una suma de fracciones es hallar el común denominador.
Conseguir un denominador común implica que lleguemos a tener dos fracciones con el mismo denominador. Lo haremos simplificando, ampliando o multiplicando los denominadores.
Luego de hallar el común denominador continuaremos con el segundo paso.
El segundo paso para resolver una adición de fracciones es sumar los numeradores.
Es probable que nos topemos con diferentes casos de sumas que estudiaremos en seguida:

Uno de los denominadores que aparecen en el ejercicio inicial será el común denominador.

A veces se nos presentarán fracciones bastante simples en las que no necesitaremos ampliar o simplificar a ambas, sino sólo a una de las fracciones.
Veamos un ejemplo:

$\frac{3}{2}+\frac{1}{4}=$

Al observar estos denominadores nos percataremos de inmediato que, si multiplicamos el denominador $2$ por $2$, llegaremos al denominador $4$.
De este modo, llegaremos al común denominador y podremos resolver el ejercicio con facilidad.

Observa -> Al multiplicar el denominador para transformarlo en común denominador, también deberemos multiplicar el numerador por el mismo número para que el valor de la fracción no cambie.

Lo haremos ampliando por $2$ y obtendremos:

$\frac{6}{4}+\frac{1}{4}=$

Ahora pasemos al segundo paso y sumemos los numeradores.
Atención –> No sumamos los denominadores. Una vez que llegamos al común denominador sólo se suman los numeradores que, de hecho, tienen el mismo denominador.

Veámoslo en un ejercicio:

$\frac{6}{4}+\frac{1}{4}=\frac{7}{4}$

Sumamos $1+6$ y dejamos el denominador una sola vez.

Si lo deseamos, podemos simplificar la fracción y escribirla del siguiente modo: $1\frac{3}{4}$

Otro ejercicio:

$\frac{1}{3}+\frac{2}{6}=$

Solución:
Nos daremos cuenta de que, si multiplicamos $3$ por $2$ llegaremos a $6$ y, éste será el común denominador.

Obtendremos:

$​​\frac{2}{6}+\frac{2}{6}=$

Sumemos los numeradores y obtendremos:
$\frac{4}{6}$
Podemos simplificar y llegar a: $\frac{2}{3}$

El común denominador será el producto de los denominadores dados.

A veces nos toparemos con ejercicios un poco más complicados en los que no será suficiente ampliar una sola fracción para conseguir el común denominador, sino que, deberemos intervenir en ambas fracciones.
No te preocupes, el modo de actuar en un caso así es, simplemente, multiplicar la primera fracción por el denominador de la segunda y, multiplicar la segunda fracción por el denominador de la primera.

Observa cuán simple es esto:

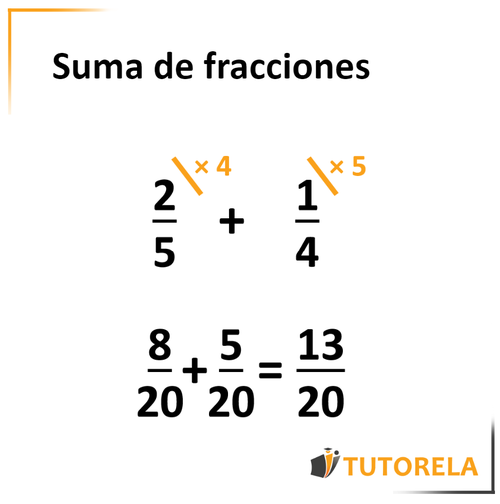
Multipliquemos los denominadores:
Multiplicaremos el $\frac{2}{5}$ por $4$ (el denominador de la segunda fracción) y el $\frac{1}{4}$ por $5$ (el denominador de la primera fracción).
Obtendremos:
$\frac{8}{20}+\frac{5}{20}=$

Sumemos los numeradores y llegaremos a la solución:
$\frac{13}{20}$
¿Viste que era simple? Éste es un método técnico que no requiere que pensemos cómo llegar al común denominador.
Por consiguiente, recomendamos utilizarlo en todos los ejercicios de adición de fracciones.

Suma de $3$ fracciones

En caso de que hubiera en el ejercicio $3$ fracciones con denominadores diferentes, primero encontraremos el común denominador a $2$ de ellos (los más sencillos), luego hallaremos el común denominador entre el que obtuvimos y el de la tercera fracción dada.

Veamos un ejemplo y verás que es muy simple:
$\frac{2}{10}+\frac{2}{3}+\frac{4}{5}=$
Miremos los denominadores y preguntémonos - Entre los tres denominadores ¿A qué par de ellos es más fácil hallar un común denominador?
La respuesta es $5$ y $10$, ya que $10$ es el común denominador de ambos.
Por consiguiente, multiplicaremos $\frac{4}{5}$ por $2$ y obtendremos:
$\frac{2}{10}+\frac{2}{3}+\frac{8}{10}=$
Ahora podemos sumar los numeradores que ya tienen común denominador para llegar a un ejercicio más claro y ordenado (este paso no es obligatorio, pero nos ayudará más tarde.

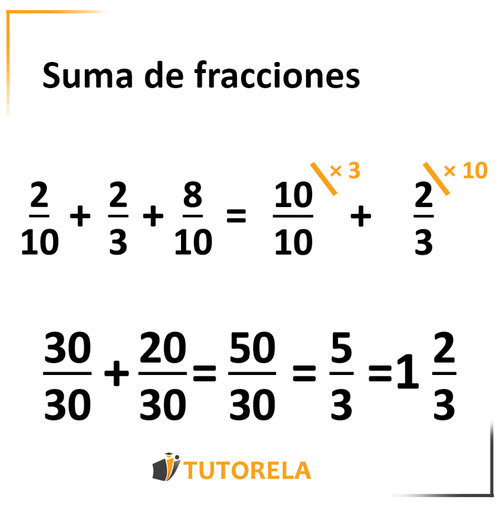
Ahora sólo queda que hallemos el común denominador entre $10$ -> el nuevo denominador que encontramos, y $3$ el tercer denominador del ejercicio.
Lo haremos con el método de la multiplicación de denominadores y obtendremos:
$\frac{30}{30}+\frac{20}{30}=$
Sumemos los numeradores y obtendremos:
$\frac{50}{30}$
Podemos simplificar y llegar a:
$\frac{5}{3}=1\frac{2}{3}$