Parte de una cantidad

Dividiremos la cantidad total por el denominador de la parte, multiplicaremos el resultado obtenido por el numerador de la parte y obtendremos la cantidad parcial.

Dividiremos el número dado (parte de una cantidad) por el numerador de la parte.
Multiplicaremos lo obtenido por el denominador de la parte y obtendremos la cantidad completa.

En el numerador - anotaremos la cantidad parcial
En el denominador - anotaremos la cantidad completa
Reduciremos la fracción que recibimos y llegar a la parte deseada.

El tema de la parte de una cantidad en fracciones es agradable y fácil si entiendes el principio y la lógica.
Por lo tanto, concéntrese y vea cómo aprende a resolver preguntas de una parte de una cantidad sin problema.
En la vida cotidiana, una cantidad entera puede ser el número de niños en una clase por ejemplo y un parte de una cantidad es el número de niños que estudian en una determinada clase.

Dividimos el tema en 3 situaciones.

Se conoce la cantidad total
y queremos saber algo específico sobre una parte de la cantidad.
Procedimiento:
Dividiremos la cantidad total por el denominador de la parte.
Multiplicaremos el resultado obtenido por el numerador de la parte y obtendremos la respuesta final.

Veamos esto mientras hacemos una pregunta:
En la clase de música hay $30$ estudiantes - esta es la cantidad completa.
$1 \over 3$ De la clase tocan la guitarra - esa es la parte específica.

¿Cuántos niños de la clase de música tocan la guitarra? – la parte de la cantidad total.

Solución:
para saber cuánto es $1 \over 3$
Dividiremos la cantidad total -> $30$ por el número $3$ (El número que aparece en el denominador de la parte.
Obtendremos:
$30:3=10$
Si multiplicamos a $10$ en el numerador de la parte -> $1$todavía queda con, $10$.

Es decir $1 \over 3$ de $30$ es $10$ niños.
También podemos ver esto en la ilustración:

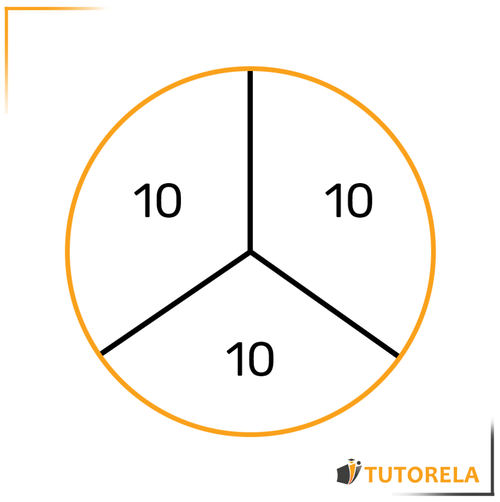
Cuando dividimos $30$ para $3$ en partes iguales, obtenemos que cada parte es igual a $10$.
Esto significa que-> $10$ niños de la clase tocan la guitarra.

Sección de bonus:  
$2 \over 3$ de la clase de música tocan la batería.
¿Cuántos niños tocan la batería?

Solución:
Ahora queremos saber cuánto es $2 \over 3$ de $30$
Revelamos que $1 \over 3$ de $30$ es $10$ niños y por lo tanto $2 \over 3$ de $30$ es $20$ niños. Es decir $20$ niños tocan la batería.
La forma principal sin depender de la primera sección:
Dividiremos la cantidad total - $30$ En el denominador de la parte -> $3$
Recibimos
$30:3=10$
El resultado $10$ que recibimos, multiplicamos el numerador de la parte -> $2$
Recibimos
$10 \times 2=20$

Respuesta:
Es decir $20$ niños tocan los tambores.

La cantidad completa es desconocida
La parte de una cantidad es conocida y dada en un número (se llama cantidad parcial).

El procedimiento es:
dividiremos el número dado (cantidad parcial) por el numerador de la parte.
Multiplicaremos lo obtenido por el denominador de la parte y obtendremos la cantidad completa.

Veamos esto mientras hacemos una pregunta:
$6$ estudiantes de la clase usan una camisa roja y componen $2 \over 5$ de la clase.
¿Cuántos niños hay en la clase?

Solución:
aquí necesitamos encontrar la cantidad completa, por lo que la resolveremos de acuerdo con los pasos anteriores.
Dividiremos el número dado (la cantidad parcial) –> $6$ por el numerador de la parte $2$ y obtenemos:
$6:2=3$
El resultado que obtuvimos $3$ lo multiplicamos por el denominador de la parte - $5$ y obtendremos la cantidad completa.
Obtenemos:
$3 \times 5=15$

Respuesta:
En la clase hay $15$ alumnos totales.

Se conoce la cantidad total
Se conoce la cantidad parcial (el número dado)
Se desconoce la parte en la fracción

El procedimiento es:

Dividiremos la cantidad parcial por la cantidad completa - usando una fracción.

Es decir:
en el numerador - anotaremos la cantidad parcial
en el denominador - anotaremos la cantidad completa
la fracción que obtuvimos, reduciremos y obtendremos la parte deseada .

Vamos a ejercitar:
$7$ niños de la clase saben hablar inglés.
En total hay $42$ niños en la clase.
¿Qué parte de la clase sabe hablar inglés?

Solución:
Anotaremos la cantidad parcial en el numerador $7$
y en el denominador anotaremos la cantidad completa $42$
Obtenemos:
$7 \over 42$
Reducimos y obtenemos:
$1 \over 6$
Respuesta:
$1 \over 6$ de los estudiantes de la clase saben hablar inglés.