Métricas claves en estadística

Frecuencia - como su nombre lo indica. Es el valor recurrente en una lista de datos en particular con mayor frecuencia. También puede haber casos en los que haya más de una frecuencia.
Promedio- se calcula dividiendo la suma de todos los datos por el número de datos. Es importante señalar que el promedio siempre se ubicará entre el valor máximo y el valor mínimo de los datos. El promedio no tiene que ser un número entero ni tiene que aparecer en la lista de datos.
Mediana - es el valor medio dentro de una lista ascendente o descendente de datos. Esto significa que el cincuenta por ciento de los datos serán mayores que la mediana y el cincuenta por ciento de los datos serán menores que la mediana. Cuando la lista de datos tiene un número par de elementos, la mediana no tiene por qué ser uno de los datos de la lista.

Ilustraremos el concepto de frecuencia usando un ejemplo

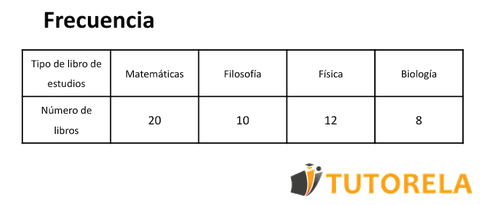
A continuación se muestra una tabla que ilustra la distribución de los libros de estudios según su asignatura. Hay un total de $50$ libros de estudios.

Se nos pide encontrar el tipo más frecuente de libros de estudios. ¿Cuántas veces aparece?

Observemos la tabla, y parece que el tipo de libro de estudios más frecuente son los libros de matemáticas. $20$ libros de estudios son de matemáticas.

Ilustraremos el concepto del promedio usando un ejemplo.

Coral compró tres pantalones a los siguientes precios: $ $150$ , $ $80$ y $ $100$ .

Se nos pide que calculemos el precio promedio que pagó Coral por unos pantalones.

Calcule el precio promedio aplicando la norma que aprendimos sobre el cálculo de promedios: divida la suma de todos los datos por la cantidad de datos.

La suma de todos los datos es: $150+80+100=330$ $

El número de datos es $3$ (un total de 3 pantalones).

Ahora obtenemos: promedio $=\frac{330}{3}=110$ $.

Es decir, el precio promedio que pagó Coral por un par de pantalones es $ $110$ . Se puede ver que el promedio en sí no aparece en absoluto en la lista de datos.

¡Únete a 30,000 estudiantes destacados en matemáticas!

Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy

Ilustraremos el concepto de mediana usando dos ejemplos

Ejemplo 1

Lista de datos:

$10,30,50,70,90$

Debemos encontrar la mediana.

Esta es una lista de números ordenados en orden ascendente (de lo contrario tendríamos que ordenarlos nosotros mismos).

El número $50$ está en una posición central, ya que nos referimos a un número impar de elementos ( $50$ ).

Por lo tanto, la mediana es $50$ .

Ejemplo 2

Lista de datos:

$10,30,50,70,90,110$

Debemos encontrar la mediana.

Esta es una lista de números ordenados en orden ascendente (de lo contrario tendríamos que ordenarlos nosotros mismos).

Esta vez nos referimos a un número par de elementos ( $6$ ), por lo que tenemos dos elementos principales: $50$ y $70$ .

Para calcular la mediana, debemos calcular el promedio de los dos números centrales.

Obtenemos: mediana $=\frac{(50+70)}{2}=\frac{120}{2}=60$

Es decir, en este caso la mediana es $60$ .

Es importante tener en cuenta que la mediana no tiene que ser uno de los datos de la lista.

Si te interesa este artículo también te pueden interesar los siguientes artículos:

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.