División acorde a una razón dada

Leo y Romi reparten entre ellos un total de $112$ canicas.

La razón entre las canicas de Leo y las de Romi es $5:3$.

¿Cuántas canicas recibió Leo y cuántas Romi?

En una pregunta de este estilo deberemos dividir la cantidad definida ($112$) según la razón dada entre Leo y Romi.

Con suma facilidad.

Podemos elegir una de las siguientes maneras:

Simplificaremos la razón dada del siguiente modo:

Por cada $5$ canicas para Leo, Romi recibirá $3$.

Por lo tanto, podremos utilizar la incógnita $X$ y escribirlo del siguiente modo:

Leo recibe $5X$ canicas

Romi recibe $3X$ canicas

Ahora, podemos tomar el dato brindado en la pregunta acerca de que el total de las canicas es $112$ y escribir una ecuación con una incógnita:

$5X+3X=112$

Despejaremos la $X$ y obtendremos:

$8X=112$

$x=14$

¡Presta atención! Aún no hemos llegado a la respuesta final.

Nos queda colocar los nuevos datos y nos dará que:

Leo recibirá $5\times14=70$

$70$ canicas

Romi recibirá $3\times14=42$

$42$ canicas

Trazaremos una tabla fija que nos ayudará a organizar los datos y a darnos la respuesta a las preguntas de este tipo:

Aprendamos con este ejemplo cómo acomodar los datos en la tabla y luego hallar la respuesta.

Pregunta:

Sharon y Ana donaron juntas a la Asociación Protectora de Animales un importe total de $400$ $.

Por cada $3$$ que donó Sharon, Ana donó $7$$.

¿Cuánto donó cada una de ellas?

Solución:

Trazaremos una tabla:

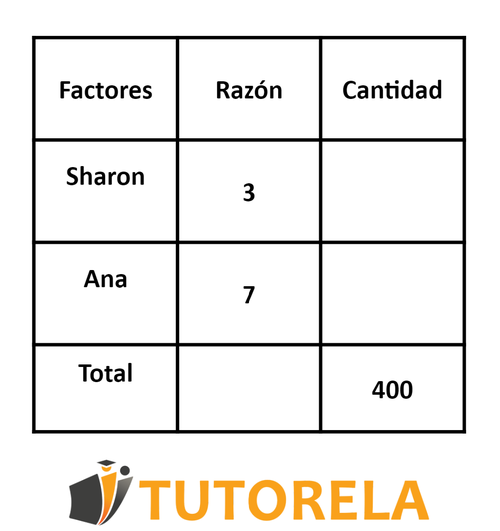
Primeramente, escribiremos lo que tenemos: Sharon y Ana.

Ahora rellenaremos el importe total: $400$$.

Luego, añadiremos la razón según los datos dados en la pregunta:

Sharon $3$, Ana $7$.

Presta atención de anotarlo bajo la columna de razón y no de la de importe ya que Sharon y Ana no donaron solamente $10$$. Se trata sólo de la razón.

Bien.

Ahora, calculemos el total de la razón: $3+7$ y nos dará:

Hemos llegado a la fase principal:

Entender cuál es la razón total dentro del importe total.

Es decir:

Cuánto es $10$ de $400$

Dividamos los $400$ por $10$ y nos dará:

$400:10=40$

Ahora que sabemos que la razón total es $40$, la aplicaremos a cada término por separado del siguiente modo:

Multiplicaremos la razón de cada término por la razón total que hallamos y obtendremos el importe.

¡Genial! Podemos tomar las respuestas de la tabla y entender que:

Sharon donó $120$$ y Ana donó $280$$.

En cierta tienda del centro comercial hay $100$ electrodomésticos, neveras y aires acondicionados.

La razón entre las neveras y los aires acondicionados es de $3:1$. 

Nosotros debemos hallar la cantidad de neveras y de aires que hay en la tienda.

En este ejercicio nuestra tarea es dividir los $100$ electrodomésticos según la razón de $3:1$.

Podemos deducir que $3$ representa la cantidad de neveras y, en cambio, $1$ representa la cantidad de aires acondicionados.

Señalemos a ambos con una variable $X$.

Tracemos una ecuación simple:

$3X+X=100$

$4X=100$

$X=25$

De aquí se desprende que la cantidad de neveras es $75 (3X)$, y la de aires acondicionados es $X=25$.

Siempre podremos volver y controlar nuestro resultado corroborando que la cantidad total de electrodomésticos en la tienda es $100$, tal como se expone en el primer dato dado.

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Razón, proporcionalidad y escala

Razón

Razones equivalentes

Proporcionalidad

Hallar un dato que falta en la proporcionalidad

Proporcionalidad directa

Proporcionalidad inversa

Escala

En la pagina web de Tutorela encontrarás una variedad de artículos con interesantes explicaciones sobre matemáticas