Para hallar la solución del sistema de ecuaciones cuadráticas (puntos de intersección de las funciones) actuaremos del siguiente modo:
Ecuaciones y sistemas de ecuaciones de segundo grado o cuadráticas
Sistema de ecuaciones cuadráticas
- Corroboraremos que la incógnita esté escrita de la misma manera en ambas ecuaciones
- Compararemos las ecuaciones
- Encontremos las
- Coloquemos paulatinamente una en una de las ecuaciones para despejar su .
- Anotemos prolijamente las respuestas que hallamos.
¡Pruébate en ecuaciones y sistemas de ecuaciones cuadráticas!
Delante de ti hay un rectángulo,
es sabido que \( x>0 \)
El área del rectángulo es \( x^2-13 \)
Halla x.
Sistema de ecuaciones cuadráticas
Ya aprendimos que no debemos temerle a la palabra «sistema». No te preocupes, aun cuando se trate de un sistema de ecuaciones cuadráticas, que no sean lineales, la solución es simple y sencilla.
Los sistemas de ecuaciones cuadráticas o de segundo grado son ecuaciones cuadráticas escritas juntas, una al lado de la otra o una debajo de la otra con un corchete rizado, similar a lo que ya estudiamos para los sistemas de ecuaciones lineales.
Por lo general, y no se nos habrían dado, por lo tanto, son nuestras incógnitas.
Cuando el problema enuncie «dado el sistema de ecuaciones» deberás saber que el resultado tiene que ser y que cumplan con las condiciones de dicho sistema.
El sistema puede tener una solución, dos soluciones o incluso ninguna.
El significado de la solución del sistema de ecuaciones lo demuestran los puntos de intersección de las funciones.
En aquellos mismos puntos las funciones se encuentran, se intersecan.
Estos mismos puntos específicos existen tanto en la primera ecuación como en la segunda.
Solución algebraica
Para resolver un sistema de ecuaciones cuadráticas haremos uso del método de comparación entre ecuaciones cuadráticas
Cuando tenemos un sistema de ecuaciones cuadráticas y la aislada de este modo (con el mismo coeficiente en ambas ecuaciones):
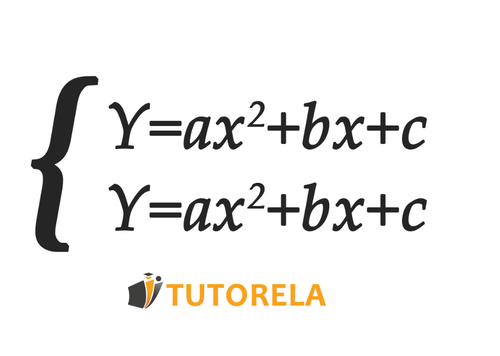
Procederemos acorde al siguiente orden:
Corroboraremos que la incógnita esté escrita de la misma manera en ambas ecuaciones
Compararemos las ecuaciones
Hallaremos las
Colocaremos paulatinamente una en una de las ecuaciones para despejar su .
Anotaremos prolijamente las respuestas halladas.
Nota
Los coeficientes de la incógnita y los diversos parámetros no deben, necesariamente, ser iguales, a excepción de la incógnita . Cuando comparas las ecuaciones corrobora, primeramente, que la incógnita esté escrita de la misma manera en ambas ecuaciones
Veamos un ejemplo de resolución de un sistema de ecuaciones con el método de comparación entre ecuaciones cuadráticas:
Dado el siguiente sistema de ecuaciones:

Actuaremos paso por paso:
- Corroboraremos que la incógnita esté escrita de la misma manera en ambas ecuaciones
La incógnita efectivamente aparece del mismo modo en ambas ecuaciones, su coeficiente es . - Compararemos las ecuaciones
- Hallaremos las
Resolveremos este ecuación como una ecuación con
incógnita:
Transpondremos miembros:
Resolveremos la ecuación cuadrática (con la fórmula cuadrática) y obtendremos:
- Colocaremos paulatinamente una en una de las ecuaciones (la original) para despejar su
Comencemos con
Colocaremos en la ecuación seleccionada dentro del sistema de ecuaciones (no importa cuál, conviene elegir la que parece ser más fácil):
Colocaremos
Obtendremos:
Escribamos este resultado:
Ahora pasemos a la segunda .
Colocaremos en la ecuación seleccionada dentro del sistema de ecuaciones (no importa cuál)
Colocaremos Recordemos utilizar paréntesis para no confundirnos con los signos de sumar y de restar
Obtendremos:
Escribamos esta solución:
5. Anotemos prolijamente las respuestas que hallamos.
Ahora pasemos al método gráfico, así entenderemos mejor el significado de la solución del sistema de ecuaciones.
Dadas 2 relaciones siguientes entre las variables x y y:
\( x^2+4=-6y \)
\( y^2+9=-4x \)
Marca la afirmación correcta:
\( \begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0 \)
Resuelve las ecuaciones anteriores completando el cuadrado/factorizando:
Asegúrate de explicar los pasos , y muestra tu trabajo: , incluyendo todos los cálculos:
\( (a+by)^2(a-by)=\text{?} \)
Delante de ti hay un rectángulo,
es sabido que \( x>0 \)
El área del rectángulo es \( x^2-13 \)
Halla x.
Solución gráfica
La solución gráfica del sistema de ecuaciones cuadráticas son los puntos de intersección de las parábolas.
Por consiguiente, cuando las parábolas están representadas gráficamente, la solución del sistema de ecuaciones serán sus puntos de intersección.
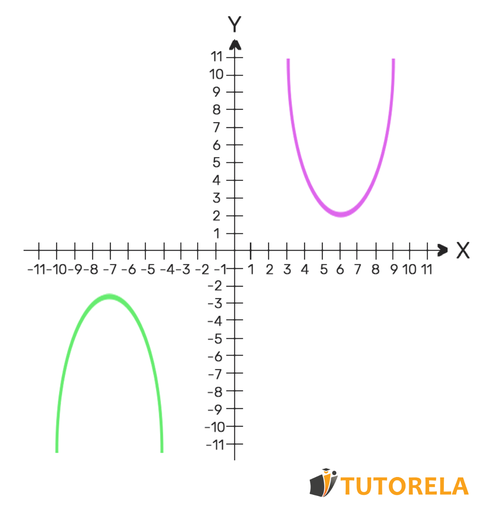
Si no se intersecan, quiere decir que el sistema de ecuaciones no tiene solución.
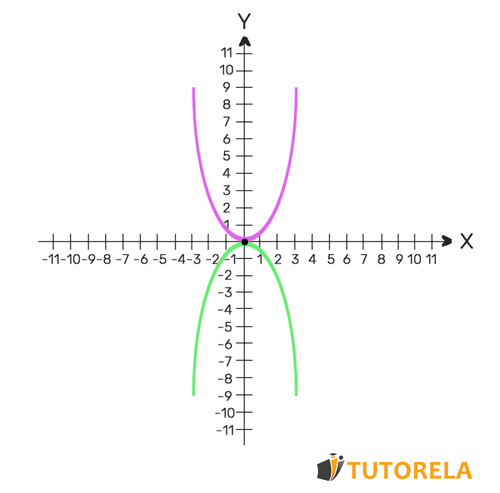
Por ejemplo
Si se cortan una vez, el sistema de ecuaciones tendrá una solución - el punto de intersección de las parábolas.
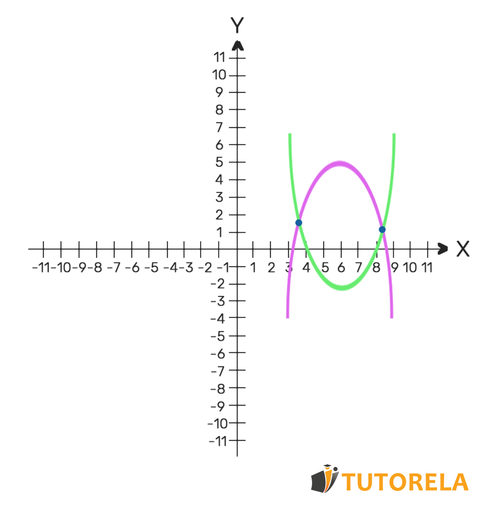
Por ejemplo
Si se intersecan dos veces, el sistema de ecuaciones tendrá dos soluciones - los puntos de intersección de las parábolas.
Por ejemplo
Ahora, pasemos al sistema de ecuaciones combinadas – o sea, un ¡a linealy la otra cuadrática.
Solución de un sistema de ecuaciones cuando una de ellas es lineal y la otra cuadrática
En caso de que el sistema de ecuaciones esté compuesto por una ecuación cuadrática y una ecuación lineal, del siguiente modo:
Utilizaremos el método de sustitución
Método de sustitución: Nos permite colocar en una ecuación el valor de la incógnita y, de este modo, conseguir una ecuación con una incógnita.
Nuevamente, recordemos colocar la incógnita entre paréntesis de forma prolija para evitar confusiones.
Nota: Se pueden ordenar las ecuaciones de un modo diferente, por ejemplo, la ecuación lineal no tiene por qué representarse del mismo modo visto anteriormente y podría tener un coeficiente que no fuera .
Veámoslo en un ejemplo:
Ejemplo de uso del método de sustitución
Dado el sistema de ecuaciones (combinadas):
Podremos percatarnos de que las ecuaciones están escritas de un modo diferente una de la otra (en una la aislada y en la otra no) y no hay ningún problema con esto.
Para utilizar el método de sustitución deberemos, por lo general, aislar totalmente una de las incógnitas de las ecuaciones.
Ahora, podemos colocar el valor de (la primera ecuación cuadrática) en la ecuación lineal y obtener una ecuación lineal con una incógnita.
Recordemos usar paréntesis para evitar confusión.
Veamos:
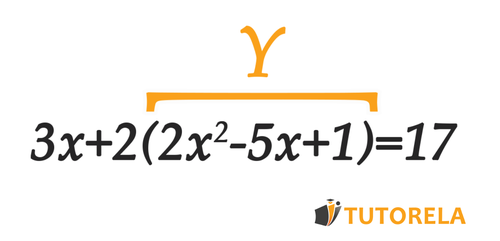
Quitemos los paréntesis y obtendremos:
Combinemos términos semejantes y obtendremos:
Ordenemos la ecuación, transpongamos miembros y obtendremos:
Resolvamos con la fórmula cuadrática y obtendremos:
Ahora, recordemos colocar los valores de las halladas para encontrar las y así poder llegar a un resultado completo.
Comenzaremos por y lo colocaremos en una de las ecuaciones originales (la que parezca más sencilla - que por lo general es la lineal)
Obtendremos:
Escribamos esta solución:
Ahora coloquemos la segunda que hallamos, en una de las ecuaciones originales y obtendremos:
Escribamos esta solución:
Anotemos prolijamente las soluciones halladas
Éstos son los puntos de intersección de la recta con la parábola.
Dadas 2 relaciones siguientes entre las variables x y y:
\( x^2+4=-6y \)
\( y^2+9=-4x \)
Marca la afirmación correcta:
\( \begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0 \)
Resuelve las ecuaciones anteriores completando el cuadrado/factorizando:
Asegúrate de explicar los pasos , y muestra tu trabajo: , incluyendo todos los cálculos:
\( (a+by)^2(a-by)=\text{?} \)
Delante de ti hay un rectángulo,
es sabido que \( x>0 \)
El área del rectángulo es \( x^2-13 \)
Halla x.
Intersección entre dos parábolas
Parábolas ubicadas en el mismo plano cartesiano pueden intersecarse más de una vez.
Para hallar los puntos de intersección entre las parábolas deberemos comparar sus ecuaciones, tal como hemos aprendido, cuando aparece del mismo modo en ambas ecuaciones (con el mismo coeficiente).
Al comparar las ecuaciones llegaremos a una ecuación con una incógnita .
Despejaremos el valor de y colocaremos alternativamente en cada una de las ecuaciones el valor de para descubrir .
Si llegamos a una solución querrá decir que las parábolas se intersecan una sola vez.
Si llegamos a dos soluciones querrá decir que las parábolas se intersecan dos veces.
Si llegáramos a que no hay solución querrá decir que las parábolas no se intersecan, no se cortan en absoluto.
Información útil
En algunos casos podría presentársenos, como en el ejemplo, que las parábolas se cortan cuando
Y la pregunta será cuáles son los puntos de intersección de las parábolas.
A fin de hallar los puntos de intersección, simplemente colocaremos en una de las ecuaciones de las parábolas dadas y así descubriremos el punto.
Problemas verbales
Debemos convertir problemas matemáticos verbales en ecuaciones cuadráticas para resolverlos
Del mismo modo que ya hemos hecho, se construyen ecuaciones en base al texto dado en el problema.
¿Cómo lo haremos?
La clave para la solución de problemas de este tipo es describir las incógnitas a través de una sola incógnita .
De este modo en lugar de llegar a dos ecuaciones con dos incógnitas llegaremos a una ecuación cuadrática.
Otra cuestión muy importante es leer y entender qué es exactamente lo que nos están diciendo en el problema. De este modo podremos construir la ecuación correctamente.
Veamos un ejemplo:
Encuentra dos números cuya suma equivalga a y la suma de éstos al cuadrado de
Solución:
Primero, definamos las variables con una incógnita
Primer número:
Segundo número:
¿Cómo hemos definido el segundo número?
Sabemos que la suma de los dos números que estamos buscando da
Pensemos esto: digamos que el segundo número fuera ,
escribiríamos
y aislaríamos la
Obtendríamos
Magnífico. Ahora pasemos a la segunda parte del problema: la suma de los números al cuadrado da Es decir, si elevamos al cuadrado a cada uno de los números y luego los sumamos obtendremos
Traduzcámoslo a una ecuación:
¡Genial! Ahora saquemos los paréntesis con le fórmula de multiplicación abreviada y llegaremos a una ecuación cuadrática ordenada:
Combinemos términos y obtendremos:
¡Genial! Podremos resolver esta ecuación cuadrática fácilmente con la fórmula cuadrática. Resolvamos y llegaremos a:
¡Presta atención! ¡Éstos no son los dos números que estamos buscando! Éstos son soluciones posibles para el primer número.
Ahora debemos encontrar cuál sería el segundo número en cada una de estas posibilidades.
Comencemos:
Cuando el primer número es ,
el segundo es y por lo tanto, .
Cuando el primer número es ,
el segundo es y por lo tanto .
Dadas 2 relaciones siguientes entre las variables x y y:
\( x^2+4=-6y \)
\( y^2+9=-4x \)
Marca la afirmación correcta:
\( \begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0 \)
Resuelve las ecuaciones anteriores completando el cuadrado/factorizando:
Asegúrate de explicar los pasos , y muestra tu trabajo: , incluyendo todos los cálculos:
\( (a+by)^2(a-by)=\text{?} \)
Delante de ti hay un rectángulo,
es sabido que \( x>0 \)
El área del rectángulo es \( x^2-13 \)
Halla x.
Desigualdad cuadrática
La desigualdad cuadrática describe en qué intervalo la función es positiva y en cuál negativa.
Ya has estudiado todos los pasos para solucionar una desigualdad de este tipo.
Antes de que comencemos a aprender cómo resolver la desigualdad cuadrática conviene que recordemos dos cosas importantes:
- Conjunto de positividad y de negatividad de la función:
Conjunto de positividad - representa las en las cuales la gráfica de la parábola se encuentra sobre el eje , con valor positivo.
Conjunto de negatividad - representa las en las cuales la gráfica de la parábola se encuentra debajo del eje , con valor negativo. - La división por un término negativo - invierte el signo de la desigualdad.
Excelente, ahora podemos comenzar.
Cuando tengamos una desigualdad cuadrática actuaremos siguiendo estos pasos:
- Transposición de miembros y aislación de la ecuación cuadrática hasta que de un lado quede . Recordemos que cuando dividimos por un término negativo se invierte la desigualdad.
- Trazado de un esquema de parábola - colocando puntos de intersección con el eje e identificación del máximo y mínimo de la parábola.
- Cálculo del intervalo correspondiente acorde al ejercicio y al esquema.
Intervalo de positividad: ecuación cuadrática
Intervalo de positividad: ecuación cuadrática
Veamos un ejemplo
Resuelve la siguiente desigualdad:
Solución:
Actuaremos paso por paso:
- Lleguemos al caso de que de un lado haya En el caso del ejemplo la ecuación está dada de este modo.
- Tracemos un esquema.
Hallemos puntos de intersección con el eje
Acorde a la fórmula cuadrática obtendremos:
Identificaremos según el coeficiente de que la parábola es la mínima.
Dibujemos un esquema
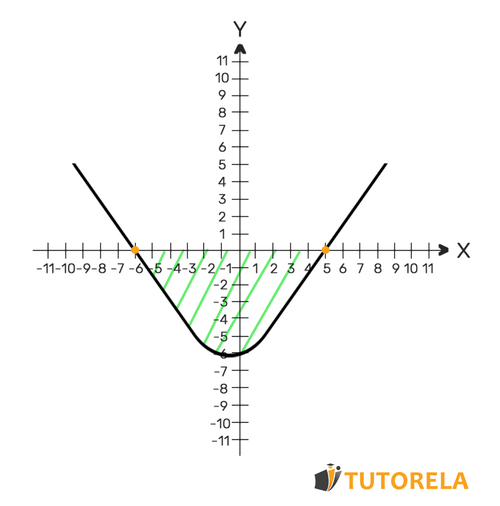
Calculemos cuál es el intervalo correspondiente acorde al ejercicio y al esquema.
Debido a que en el ejercicio preguntan cuándo la ecuación cuadrática es menor que , están preguntando sobre el intervalo de negatividad, por lo tanto, observando el esquema podremos determinar que la ecuación cuadrática es inferior a cuando :
Ésta es la solución de la desigualdad.
Ejemplos y ejercicios con soluciones de sistemas de ecuaciones cuadráticas
Ejercicio #1
Delante de ti hay un rectángulo,
es sabido que
El área del rectángulo es
Halla x.
Solución en video
Respuesta
Ejercicio #2
Dadas 2 relaciones siguientes entre las variables x y y:
Marca la afirmación correcta:
Solución en video
Respuesta
Dadas 2 relaciones siguientes entre las variables x y y:
\( x^2+4=-6y \)
\( y^2+9=-4x \)
Marca la afirmación correcta:
\( \begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0 \)
Resuelve las ecuaciones anteriores completando el cuadrado/factorizando:
Asegúrate de explicar los pasos , y muestra tu trabajo: , incluyendo todos los cálculos:
\( (a+by)^2(a-by)=\text{?} \)
Delante de ti hay un rectángulo,
es sabido que \( x>0 \)
El área del rectángulo es \( x^2-13 \)
Halla x.
- Sistema de dos ecuaciones lineales con dos incógnitas
- Resolución algebraica para un sistema de ecuaciones lineales con dos incógnitas
- Resolución con el método de sustitución para sistemas de dos ecuaciones lineales con dos incógnitas
- Resolución con el método de igualación para sistemas de dos ecuaciones lineales con dos incógnitas
- Ecuación lineal con dos incógnitas
- Solución con método gráfico para un sistema de ecuaciones lineales con dos incógnitas
- Resolución de problemas verbales con un sistema de ecuaciones lineales
- Solución de un sistema de ecuaciones cuando una de ellas es lineal y la otra cuadrática
- Problemas verbales
- La función cuadrática
- Desigualdad cuadrática
- Parábola
- Simetría
- Principales soluciones de una función cuadrática
- Trinomio al cuadrado
- La fórmula cuadrática
- Resolviendo un Sistema de Ecuaciones Lineales con Dos Variables Usando el Método Algebraico
- Propiedades de las Raíces de Ecuaciones Cuadráticas - Fórmulas de Vieta
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









