Solución de un sistema de ecuaciones cuando una de ellas es lineal y la otra cuadrática

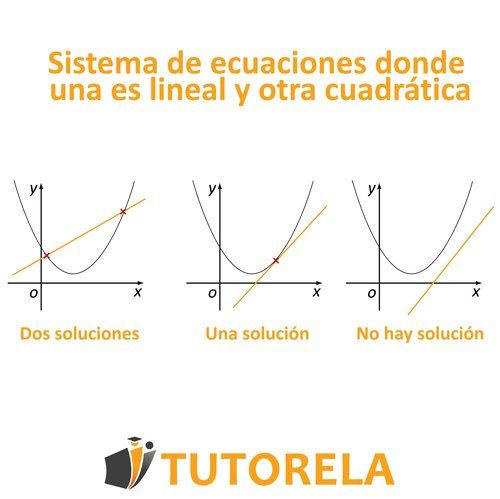
Cuando tengamos un sistema de ecuaciones donde una de las ecuaciones sea lineal y la otra cuadrática
haremos uso del método de sustitución:

Aislaremos una incógnita de una ecuación, colocaremos en la segunda ecuación el valor de la expresión de la incógnita que hemos aislado y, de este modo, obtendremos una ecuación con una incógnita. Despejaremos la $X$ o la $Y$ y luego la colocaremos en una de las ecuaciones originales para hallar el punto completo. El punto que descubramos será el punto de intersección de la recta con la parábola, y también será la solución del sistema de ecuaciones.

Dado el siguiente sistema de ecuaciones: $y=x^2+2x+7$,$2x+y=4$

Solución:
Aislemos alguna incógnita de una de las ecuaciones:
$2x+y=4$
$y=-2x+4$

Ahora, coloquemos el valor que aislamos en la segunda ecuación. Obtendremos:

$-2x+4=x^2+2x+7$

Combinemos términos semejantes y transpongamos miembros. Obtendremos:
$-X^2-4x-3=0$
Lo resolveremos con la ayuda de la fórmula cuadrática y obtendremos:
$X=-1 ,-3$
Ahora colocaremos paulatinamente una $X$ que hallamos en una de las ecuaciones para encontrar los puntos completos: Comencemos por $X=-1$

$2\times(-1)+y=4$
$-2+y=4$
$y=6$
Escribamos esta solución $(-1,6)$
pasemos a la segunda $X$ que hemos encontrado $X=-3$ y obtendremos:
$2*(-3)+y=4$
$-6+y=4$
$y=10$ escribamos esta solución $(-3,10)$

Estas soluciones son los puntos de intersección de la parábola con el eje.

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Las funciones y=x²

Familia de las parábolas y=x²+c : Desplazamiento vertical

Familia de las parábolas y=(x-p)²

Familia de las parábolas y=(x-p)²+k (combinación de desplazamiento horizontal y vertical)

Forma vértice de la función cuadrática

Forma factorizada de la función cuadrática

Completar el cuadrado en una ecuación cuadrática

Forma estándar de la función cuadrática

Sistema de ecuaciones cuadráticas - Solución algebraica y gráfica

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.