Desigualdad cuadrática

La desigualdad cuadrática nos muestra en qué intervalo la función es positiva y en cuál negativa - según el símbolo de desigualdad. Para resolver desigualdades cuadráticas de modo correcto es conveniente recordar dos cosas:

Conjunto de positividad y de negatividad de la función:
Conjunto de positividad - representa las $X$ s en las cuales la gráfica de la parábola se encuentra sobre el eje $X$ , con valor $Y$ positivo.
Conjunto de negatividad - representa las $X$ s en las cuales la gráfica de la parábola se encuentra debajo del eje $X$ , con valor $Y$ negativo .
La división por un término negativo - invierte el signo de la desigualdad.

Método para resolver la desigualdad cuadrática:

Llevaremos a cabo transposición de miembros y aislaremos la ecuación cuadrática hasta que de un lado quede 0. Recordemos que cuando dividimos por un término negativo se invierte la desigualdad.
Tracemos un esquema de la parábola - colocando puntos de intersección con el eje $X$ e identificación del máximo y mínimo de la parábola.
Calculemos cuál es el intervalo correspondiente según el ejercicio y el esquema.
Ecuación cuadrática $>0∶$ Conjunto de positividad
Ecuación cuadrática $<0∶$ Conjunto de negatividad

Explicación completa

Ir a prácticas

¡Pruébate en desigualdad cuadrática!

Resuelve la siguiente ecuación:

$$ x^2+4>0 $$

Quiz y otros ejercicios

Veamos un ejemplo de desigualdad cuadrática

$3x(x+1)<2(x^2+15)+2x$

Solución:
Progresaremos paso a paso:

1) Hagamos transposición de miembros y aislemos la ecuación cuadrática hasta que de un lado quede $0$ . Recordemos que cuando dividimos por un término negativo se invierte la desigualdad.
En el primer paso dejaremos $0$ de un lado de la ecuación.
Observa que, en este ejercicio, primero deberemos resolver lo que aparece entre paréntesis.
Abriremos los paréntesis y obtendremos:
$3x^2+3x>2x^2+30+2x$

Ahora transpongamos miembros y obtendremos:
$X^2+X-30>0$

Magnífico. Hemos dejado $0$ de un lado. Continuemos al segundo paso.

2) Tracemos un esquema de la parábola - colocando puntos de intersección con el eje $X$ e identificación del máximo y mínimo de la parábola.

Encontremos los puntos de intersección de la función con el eje $X$ :
Según la fórmula cuadrática obtendremos:

$X=5,-6$

Veremos que el extremo de la función es el mínimo (sonrisa) ya que el coeficiente de $X^2$ es positivo.
Tracemos un esquema:

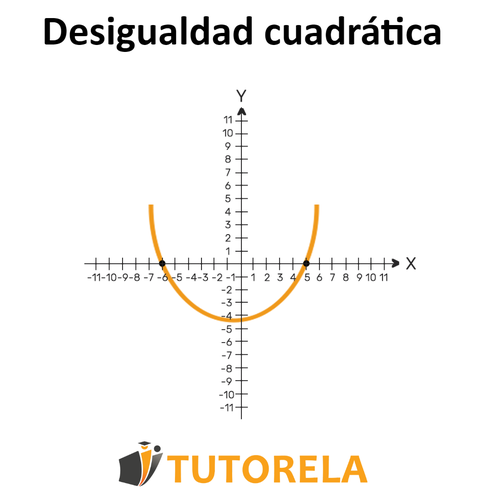
3) Calculemos cuál es el intervalo correspondiente según el ejercicio y el esquema.
En el ejercicio llegamos a la siguiente ecuación:
$X^2+X-30>0$
Es decir, buscamos los intervalos en los cuales la función es mayor que $0$ . Su conjunto de positividad.

Nos preguntaremos: ¿En qué intervalos la función es positiva? ¿En qué $X$ s la gráfica de la función está sobre el eje de la $X$ ?
La respuesta es cuando
$X>5$
$X<-6$