Sistema de ecuaciones cuadráticas - Solución algebraica y gráfica

En el sistema de ecuaciones cuadráticas deberemos hallar las $X$ y $Y$ que cumplen con la primera ecuación y también con la segunda. El sistema puede tener una solución, dos soluciones o incluso ninguna. En el concepto de la solución del sistema de ecuaciones destacan los puntos de intersección de la función. En los mismos puntos que encontraremos - las funciones se intersecan. Si se encuentra una solución - las funciones se cortan una sola vez. Si se encuentran dos soluciones - las funciones se cortan dos veces. Si no se encuentra ninguna solución - las funciones no se cortan nunca.

Método: Comparación entre ecuaciones cuadráticas

Cuando tenemos un sistema de ecuaciones cuadráticas y la $Y$ se aísla de este modo (con el mismo coeficiente en ambas ecuaciones):
$Y=ax^2+bx+c$
$Y=ax^2+bx+c$

Procederemos según el siguiente orden:

1. Corroboraremos que la incógnita $Y$ esté escrita del mismo modo en las dos ecuaciones
2. Compararemos las ecuaciones 
3. Despejaremos las $X$ s
4. Colocaremos paulatinamente $X$ s en una de las ecuaciones para despejar su $Y$
5. Anotaremos prolijamente las soluciones que hemos encontrado.

Atención - Los otros parámetros no tiene que ser iguales necesariamente. Sólo la $Y$ debe estar aislada del mismo modo para poder equiparar las ecuaciones.

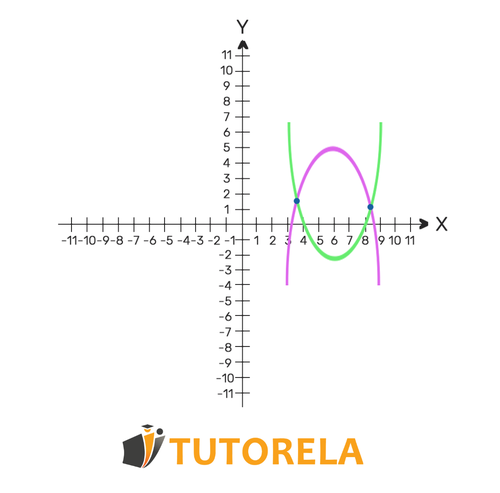
La solución del sistema de ecuaciones cuadráticas representa los puntos de intersección de las parábolas. Por lo tanto, podremos ver la solución del sistema de ecuaciones de forma gráfica como los puntos de intersección de las parábolas.

$y=5x^2-2x+6$
$y=-5x^2-2x+6$

1. Corroboremos que la $Y$ esté realmente aislada del mismo modo.
2. Comparemos las ecuaciones:
   $5x^2-2x+6=-5x^2-2x+6$
3. Despejemos las $X$ s
   $5x^2-2x+6=-5x^2-2x+6$
   Hagamos transposición de términos y obtendremos:
   $10x^2=0$
   $x^2=0$
   $x=0$
4. Hallemos la $Y$ al colocar la $X$ que hemos encontrado en una de las ecuaciones:
   $y=5x^2-2x+6$
   $y=5*0^2-2*0+6$
   $y=6$
5. Anotemos la solución que hallamos: $(6, 0)$
   en este punto se cortan las funciones y esa es la solución del sistema de ecuaciones.

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Las funciones y=x²

Familia de las parábolas y=x²+c : Desplazamiento vertical

Familia de las parábolas y=(x-p)²

Familia de las parábolas y=(x-p)²+k (combinación de desplazamiento horizontal y vertical)

Forma vértice de la función cuadrática

Forma factorizada de la función cuadrática

Completar el cuadrado en una ecuación cuadrática

Forma estándar de la función cuadrática

Solución de un sistema de ecuaciones cuando una de ellas es lineal y la otra cuadrática

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.