Para ubicar fracciones en la recta numérica llevaremos a cabo varios pasos.
Ubicación de fracciones en la recta numérica
Ubicación de fracciones en la recta numérica
Primer paso – Descubrir el valor de los arcos
Restaremos dos números dados y guardemos la diferencia.
Contaremos la cantidad de arcos que hay entre los números.
Dividiremos el resultado de la resta por la cantidad de arcos y descubriremos cuánto mide cada arco.
Segundo paso – Ubicar los números en la recta
Según la cantidad de arcos, se puede ampliar o reducir.
¡Pruébate en fracción en el eje numérica!
¿Qué número está marcado en el eje numérico?
Fracciones en la recta numérica
En este artículo aprenderemos a ordenar fracciones sobre la recta numérica, con facilidad, rapidez y sin inconvenientes.
Primero observemos la recta numérica y analicémosla.
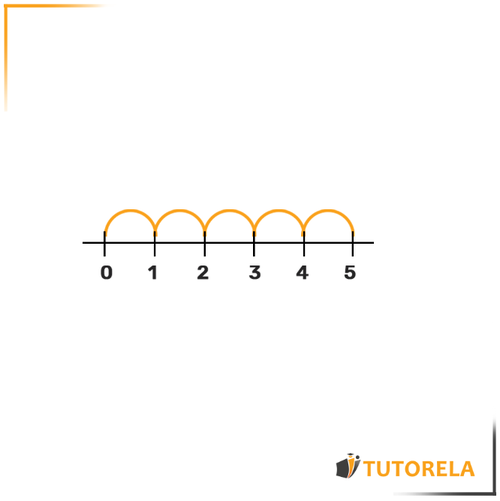
Aquí vemos una recta numérica de hasta .
Vemos que la recta se divide en y cada arco indica un aumento de .
En cambio, si observamos esta recta numérica:
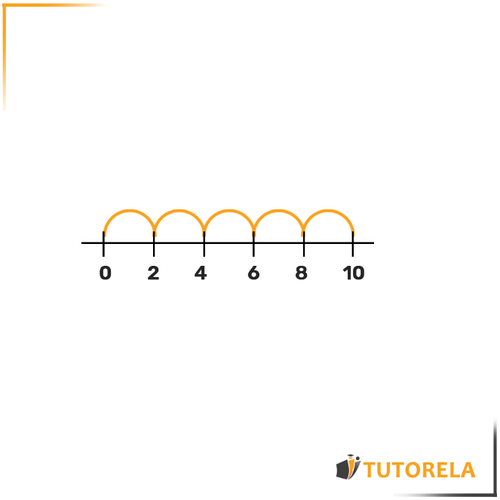
Veremos que cada arco indica un aumento de .
Para ubicar fracciones en la recta numérica lo primero que deberemos saber es cuánto se aumenta de arco en arco.
Las líneas que limitan cada arco en la recta numérica se llaman puntos. También se acostumbra a decir que – representa el espacio entre los dos puntos.
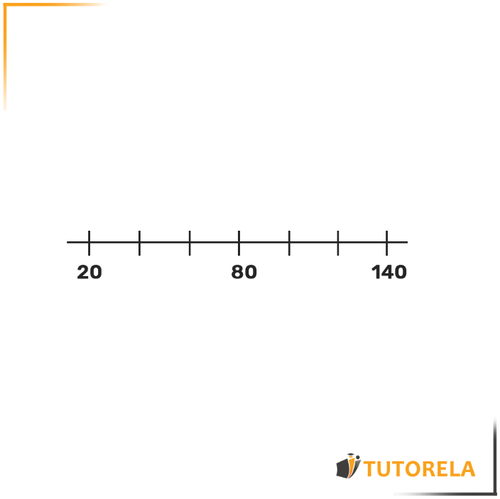
Ejercitación
Completa los números faltantes en la recta numérica:
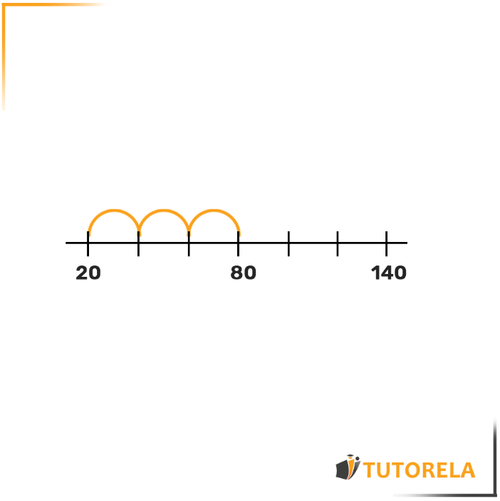
Solución:
Para poder completar los números, primero señalaremos, con un arco, los espacios que hay entre los puntos de los dos números dados
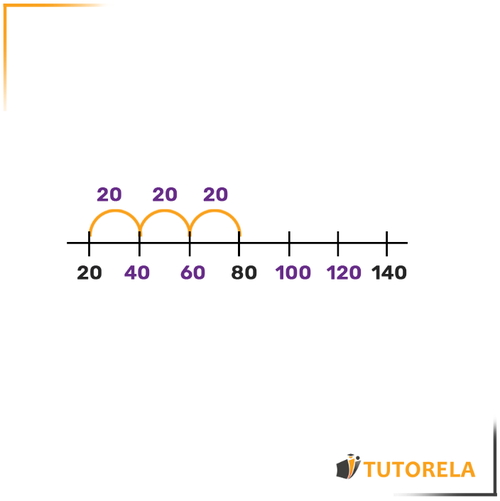
Nos percataremos de que hay arcos entre el número y
Recordemos que todos los espacios son idénticos.
Restemos
es el espacio total.
Ya que hay arcos dividiremos el por y, de este modo, llegaremos a la medida de cada arco.
Obtendremos que:
Por lo tanto, cada arco mide .
Colocaremos marcas en la recta numérica para poder completar los números restantes con suma facilidad:
Ahora que ya sabemos un poco más acerca de la recta numérica y aprendimos cómo descubrir la distancia entre los dos puntos podemos avanzar.
¿Qué número está marcado en el eje numérico?
¿Qué número está marcado en el eje numérico?
¿Qué número está marcado en el eje numérico?
Fracciones en la recta numérica
Primer paso
Descubrir la medida del arco entre dos puntos del siguiente modo:
Restar dos números dados y guardar la diferencia.
Contar la cantidad de arcos que hay entre los números.
Dividir el resultado de la resta por la cantidad de arcos y descubrir cuánto mide cada arco.
Segundo paso
Ubicar los números: Se puede aplicar reducción y amplificación si fuere necesario.
Sigamos aprendiendo con un ejemplo
Coloca las fracciones y en la recta numérica.
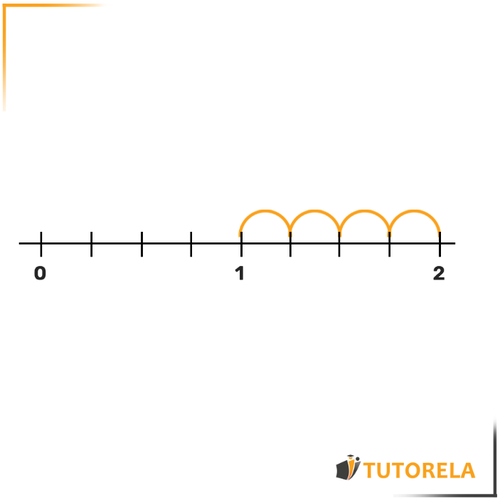
Nos preguntaremos ¿Qué diferencia hay entre los números dados?
Por ejemplo, entre y ?
La diferencia es .
¿Cuántos arcos hay entre y ?
arcos.
Dividiremos la diferencia que calculamos entre la cantidad de arcos y obtendremos:
Cada arco mide
Ahora pensemos dónde ubicar el .
Podemos amplificar el en y nos dará que .
Por lo tanto, se ubicará aquí:
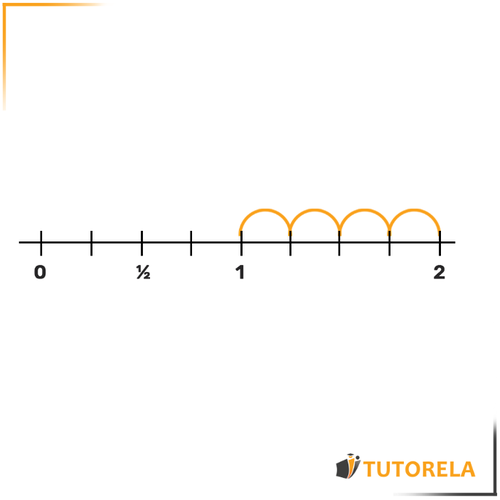
Ahora pasemos a
Vemos que hay un número entero en la fracción, por lo tanto, el número se ubicará entre y
Vimos que cada arco mide y dedujimos que equivale a .
Por consiguiente, se ubicará aquí:
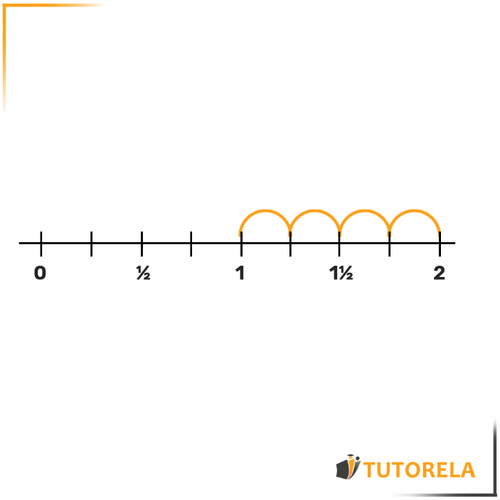
¿Qué número está marcado en el eje numérico?
¿Qué números aparecen en la recta numérica?
¿Qué número está marcado en el eje numérico?
Otro ejercicio
Halla el número que representa la flecha:
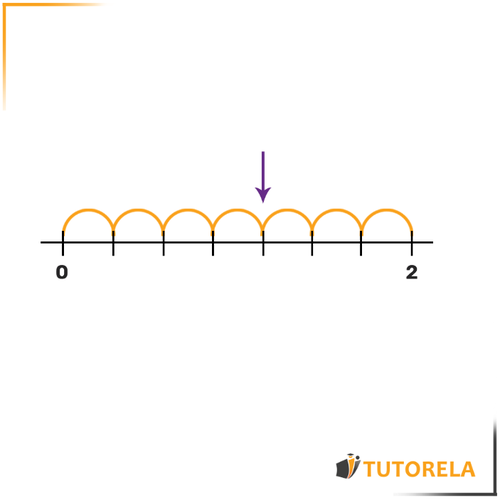
Solución:
Primero descubramos cuánto mide cada arco.
Tomemos los dos números dados y
y contemos cuántos arcos hay entre ellos.
Hay arcos entre el y el
Restemos:
Y dividamos por
Cada arco representa
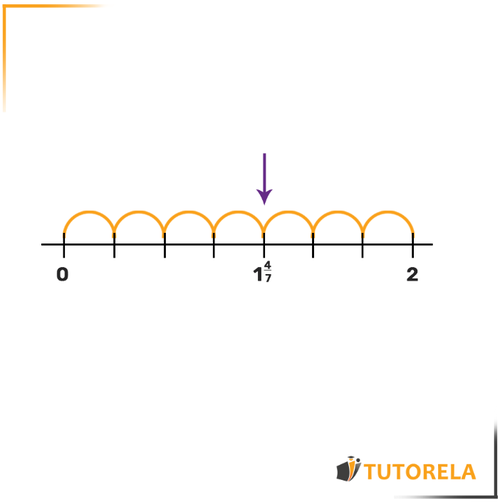
Ahora veamos cuántos arcos tenemos que saltar hasta llegar a la flecha:
La respuesta es entonces el número será
Presta atención de no olvidar al número entero .
Ejemplos y ejercicios con soluciones de ubicación de fracciones en la recta numérica
Ejercicio #1
¿Qué número está marcado en el eje numérico?
Solución en video
Respuesta
Ejercicio #2
¿Qué número está marcado en el eje numérico?
Solución en video
Respuesta
Ejercicio #3
¿Qué número está marcado en el eje numérico?
Solución en video
Respuesta
Ejercicio #4
¿Qué número está marcado en el eje numérico?
Solución en video
Respuesta
Ejercicio #5
¿Qué números aparecen en la recta numérica?
Solución en video
Respuesta
¿Qué número aparece en la recta numérica?
¿Qué número está marcado en el eje numérico?
¿Qué número está marcado en el eje numérico?
- Jerarquía de operaciones: suma, resta, multiplicación y división
- Jerarquía de operaciones: potencias
- Jerarquía de operaciones: (raíces)
- División y línea de fracción
- Los números 0 y 1 en las operaciones
- Elemento neutro / Elementos neutros
- Jerarquía de operaciones con paréntesis
- Números opuestos
- Eliminación de paréntesis en números reales
- Suma y resta de números reales
- Multiplicación y división de números reales
- Inverso multiplicativo
- Potenciación de números enteros
- Números positivos, negativos y el cero
- La recta real o La recta numérica
- Orden o jerarquía de las operaciones con fracciones
- Fracciones
- Una fracción como divisor
- ¿Como se simplifican las fracciones?
- Simplificación y amplificación de fracciones simples
- Denominador común
- Centésimas y milésimas
- Parte de una cantidad
- Suma de fracciones
- Resta de fracciones
- Multiplicación de fracciones
- División de fracciones
- Numerador
- Denominador
- Fracciones decimales
- Significado del número decimal
- Reducción y amplificación de números decimales
- Suma y resta de números decimales
- Comparación de números decimales
- Conversión de número decimal a fracción
- Residuo de una fracción









