Simetría del rombo

Antes de que hablemos sobre la simetría del rombo recordemos que tenemos dos tipos de simetría. Simetría especular y simetría rotacional.

La figura con simetría especular es una figura que, al plegar la y dividirla verticalmente en dos partes por el eje central, sus mitades coincidirían con exactitud.

La figura con simetría rotacional es una figura que «se encubre», coincide consigo misma, más de una vez, al realizar una rotación completa.

El rombo tiene simetría especular y, también, simetría rotacional.

El eje de simetría del rombo pasa por todo par de ángulos opuestos.

Como bien sabemos,

si podemos dibujar una línea vertical y plegar la figura a lo largo para obtener dos partes que se fusionarán entre ellas, la figura se considerará simétrica.

Podemos atravesar el rombo con ejes de simetría por cada par de ángulos opuestos.

Tracemos una línea de simetría vertical por un par de ángulos opuestos y podremos ver claramente que se crean dos secciones y, cuando plegamos el rombo por este eje, las secciones se unen exactamente una con la otra.

Un genial manera de demostrarlo es a través de la congruencia de los dos triángulos que se crearon por el teorema de congruencia LLL.

En el rombo todos los lados son iguales y la línea de simetría es un lado en común.

Recordemos que el orden de simetría es la cantidad de veces que todas las partes de cierta figura coinciden al hacerla girar una vuelta completa.

Veámoslo en la ilustración:

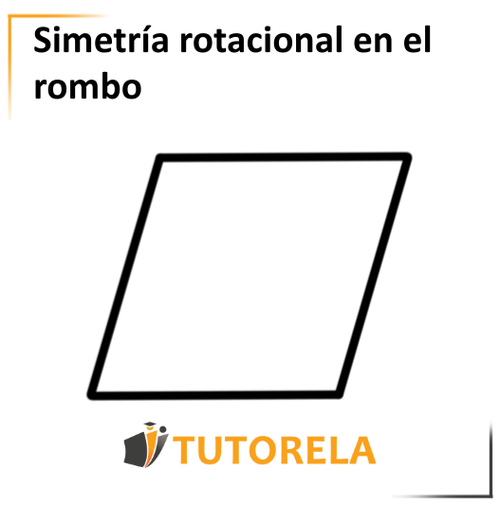
Si lo hacemos girar un cuarto de vuelta aún no coincidirá.

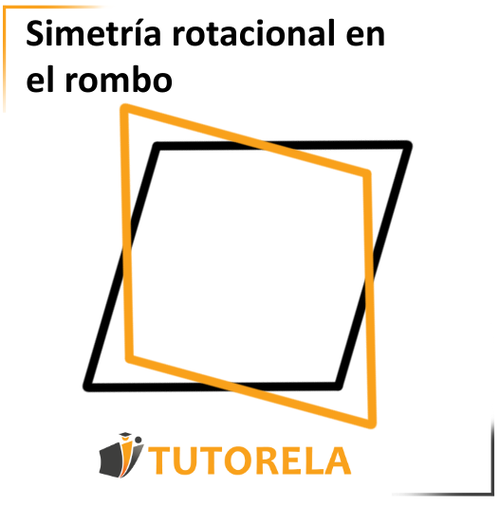
Ahora, hagámoslo rotar otro cuarto de vuelta,

es decir, ya dimos medio giro, y veamos cómo coinciden todas sus partes, se encubre.

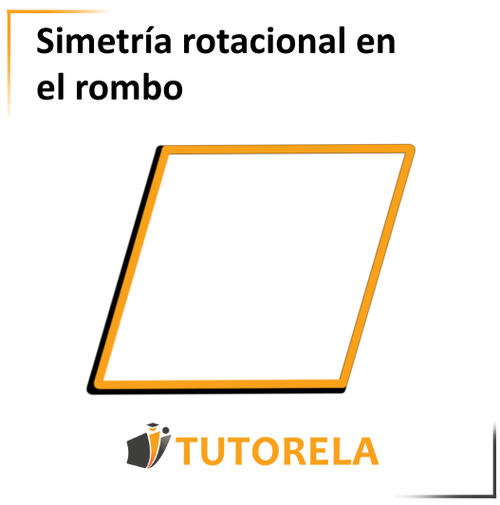
Ya en esta fase podremos determinar que el rombo tiene simetría rotacional. Aún no giró una vuelta completa y ya hubo coincidencia.

Sigamos ahora al giro completo para descubrir el orden de simetría del rombo.

Si seguimos girándolo otro cuarto de vuelta el rombo no coincidirá.

Si seguimos girándolo otro cuarto de vuelta, de hecho, ya tendremos una vuelta completa, el rombo nuevamente se verá encubierto, coincidirá con su forma original, y ésta será la segunda vez que lo hace en un giro.

Por consiguiente, podremos determinar que el rombo tiene simetría rotacional de segundo orden.

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Paralelogramo - Comprobación del paralelogramo

El área del paralelogramo: ¿qué es y cómo se calcula?

Maneras de identificar paralelogramos

Simetría en trapecios

¿Cómo se calcula el área de un rombo?

Diagonales de un rombo

De paralelogramo a rombo

Simetría

Simetría rotacional en paralelogramos

Simetría en trapecios

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.