El trapecio isósceles es, de hecho, un trapecio (es decir, un polígono de cuatro lados que dos de ellos - las bases - son paralelos), con dos de sus lados equivalentes y con sus ángulos base de igual magnitud.
Trapecio isósceles
Trapecio isósceles
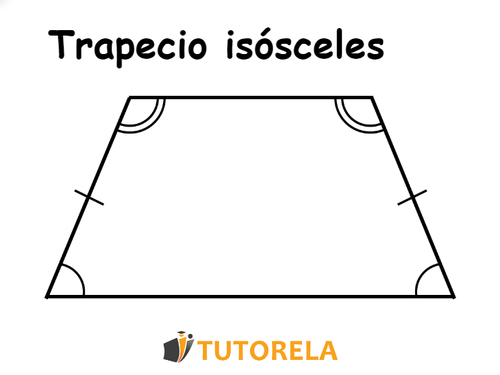
En el trapecio hay, como es sabido, dos bases y, cada base tiene dos ángulos base adyacentes a ambos lados. En otras palabras, en el trapecio isósceles hay dos juegos de ángulos de base iguales, tal como se puede apreciar en la siguiente ilustración:
¡Pruébate en trapecio isósceles!
¿En el trapecio isósceles los dos pares de lados son paralelos?
Definición del trapecio isósceles
El trapecio isósceles es, de hecho, un trapecio (es decir, un polígono de cuatro lados que dos de ellos - las bases - son paralelos), con dos de sus lados equivalentes y con sus ángulos base de igual magnitud.
En el trapecio hay, como es sabido, dos bases y, cada base tiene dos ángulos base adyacentes a ambos lados. En otras palabras, en el trapecio isósceles hay dos juegos de ángulos de base iguales, tal como se puede apreciar en la siguiente ilustración:

Propiedades del trapecio isósceles
Las propiedades detalladas aquí son las características exclusivas de los trapecios isósceles entre todos los demás tipos de trapecios. La siguiente ilustración describe los teoremas de la mejor manera:
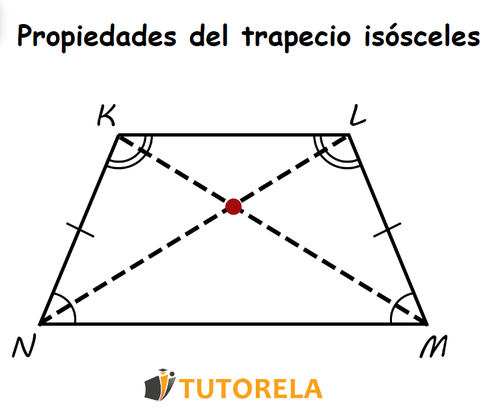
- Los lados que no son paralelos son congruentes, es decir, tienen la misma medida. Es decir, se cumple:
- En el trapecio isósceles hay dos juegos de ángulos iguales para la base mayor y para la base menor.
Es decir, los ángulos y son equivalentes, al igual que los ángulos y que también lo son.
- Las dos diagonales del trapecio isósceles son iguales. Es decir, se cumple:
- Se puede inscribir todo trapecio isósceles en una circunferencia
¿En todos los trapecios isósceles las Ángulos de la Base son iguales?
\( ∢D=50° \)
El trapecio isósceles
Cuál es \( ∢B \)?
Dado: \( ∢C=2x \)
\( ∢A=120° \)
trapecio isósceles.
Halla a x.
Demostración del trapecio isósceles
Para demostrar que un trapecio es isósceles debemos hacer uso de las propiedades especificadas anteriormente, de hecho, se trata de teoremas recíprocos. Es suficiente demostrar sólo una propiedad.
Es decir, si demostramos que:
- Los dos lados que no son paralelos son congruentes
o
- Los ángulos de la base del trapecio son congruentes
o
- Las diagonales del trapecio son congruentes
entonces, dicho trapecio es un trapecio isósceles.
Las diagonales de un trapecio isósceles
Las siguientes propiedades están referidas a las diagonales del trapecio isósceles. Para remarcar estas propiedades del mejor modo utilizaremos esta ilustración:
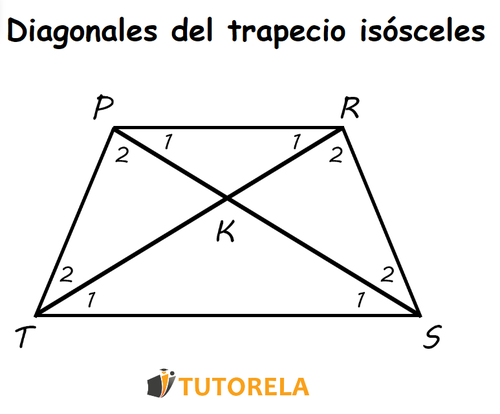
- Las dos diagonales son iguales. Es decir, se cumple:
- Los triángulos y son congruentes acorde al teorema de congruencia lado - lado - lado
- Los triángulos y son congruentes acorde al teorema de congruencia lado - lado - lado
- Los triángulos y son triángulos isósceles con todo lo que esto implica
- Los ángulos , , y son equivalentes
Dado: \( ∢A=120° \)
El trapecio isósceles
Halla a: \( ∢C \)
¿Las diagonales del trapecio necesariamente se cruzan entre sí?
En un trapecio isósceles, ¿la suma de los ángulos opuestos siempre será 180°?
Cálculo del área del trapecio isósceles
El cálculo del área de un trapecio isósceles se hace exactamente del mismo modo que se calcula el área de cualquier otro trapecio.
Es decir, se suman las longitudes de las dos bases, se multiplica el total de la suma por la altura y luego, se divide por .
Utilizaremos esta ilustración para explicar los pasos del cálculo:
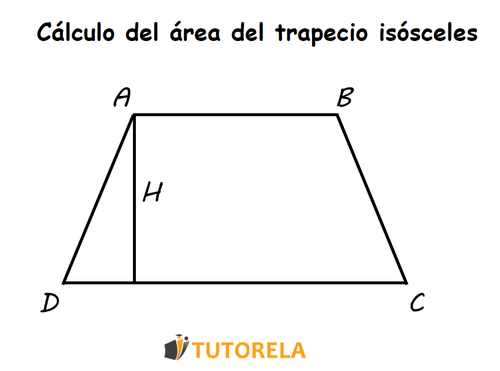
La fórmula para calcular el área del trapecio isósceles (no exclusivamente) es:
Ejemplos y ejercitación con trapecios isósceles
Ejercicio No 1
Dado el trapecio isósceles descrito en el siguiente esquema.
Se sabe que, la suma de tres ángulos da grados.
Acorde a los datos debemos calcular todos los ángulos de este trapecio isósceles.
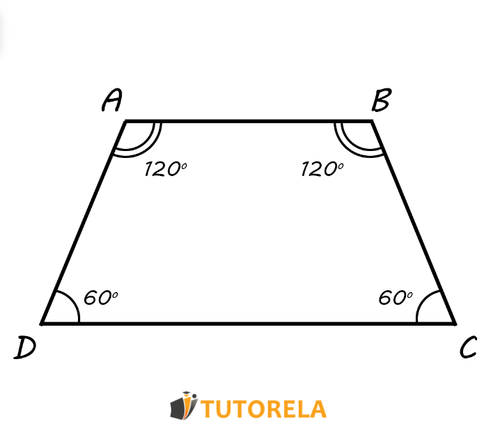
Solución:
Si la suma de los tres ángulos del trapecio dado es y la suma total de los ángulos de un trapecio (como de todo cuadrilátero) es , podemos deducir que el cuarto ángulo mide grados.
Se trata de uno de los ángulos adyacentes a la base menor, supongamos el ángulo . Ya que se trata de un trapecio isósceles, los ángulos de la base son congruentes, por lo tanto, también el ángulo mide .
Recordemos que se trata de un trapecio y que las bases y son paralelas, es decir, los ángulos y (al igual que y ) son ángulos colaterales y, por lo tanto, se complementan y juntos miden grados. Por lo tanto, nos dará que los ángulos y miden grados.
Respuesta:
Los ángulos del trapecio son
¿Las diagonales de un trapecio isósceles son iguales y se cortan entre sí?
Dado que: el perímetro del trapecio es igual a 22 cm
AB= 7 cm
AC= 3 cm
BD= 3 cm
Halla el tamaño de CD.
Dado: trapecio isósceles.
\( ∢B=3x \)
\( ∢D=x \)
Halla a \( ∢B \)
Ejercicio No 2
Dado el trapecio isósceles descrito en el siguiente esquema.
Se sabe que, la suma de dos de sus lados da .
Acorde a los datos debemos calcular todos los ángulos de este trapecio isósceles.
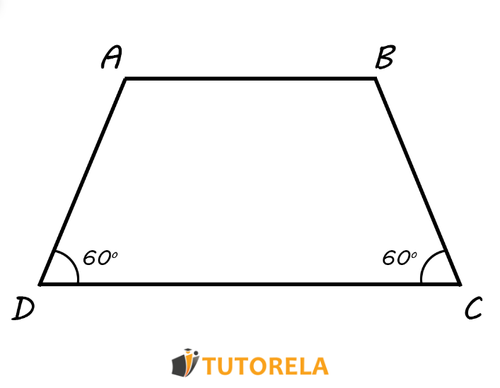
Solución:
Volvamos a las reglas relacionadas con la base y recordemos que se trata de un trapecio y que las bases y son paralelas, es decir, los ángulos y (al igual que y ) son ángulos colaterales y, por lo tanto, se complementan y juntos miden grados. Dado que la amplitud que tenemos es grados, podemos deducir que no se trata de ángulos adyacentes al mismo lado (o sea, unilaterales), sino de ángulos que comparten la misma base.
Por tratarse de un trapecio isósceles los ángulos de la base son congruentes, por consiguiente, cada uno de ellos mide grados.
El ángulo complementario (para llegar a grados) de cada uno de estos ángulos mide grados.
Respuesta:
Los ángulos del trapecio son
Ejemplos y ejercicios con soluciones de trapecio isósceles
Ejercicio #1
¿En todos los trapecios isósceles las Ángulos de la Base son iguales?
Solución en video
Solución Paso a Paso
La respuesta es sí, ya que según la ley en todo trapecio isósceles los ángulos de la base son iguales entre sí.
Respuesta
Verdadero
Ejercicio #2
Dado:
trapecio isósceles.
Halla a x.
Solución en video
Solución Paso a Paso
Dado que el trapecio es isósceles y los ángulos en ambos lados son iguales, se puede argumentar que:
Sabemos que la suma de los ángulos de un cuadrilátero es 360 grados.
Por lo tanto podemos crear la fórmula:
Reemplazamos de acuerdo a los datos existentes:
Dividimos las dos secciones por 4:
Respuesta
30°
Ejercicio #3
¿Las diagonales del trapecio necesariamente se cruzan entre sí?
Solución Paso a Paso
Las diagonales de un trapezoide isósceles son siempre iguales entre sí,
pero no necesariamente se cruzan entre sí.
(Recordatorio, "cruce" significa que se encuentran exactamente en el medio, lo que significa que están cortados en dos partes iguales, dos mitades)
Por ejemplo, se traza el siguiente trapecio ABCD, que es isósceles.
Usando un programa de computadora calculamos el centro de las diagonales,
Y observamos que los puntos centrales no son G, sino los puntos E y F.
Eso significa que las diagonales no se cruzan.

Respuesta
No verdadero
Ejercicio #4
Dado que: el perímetro del trapecio es igual a 22 cm
AB= 7 cm
AC= 3 cm
BD= 3 cm
Halla el tamaño de CD.
Solución en video
Solución Paso a Paso
Como nos dan el perímetro del trapecio y no la longitud de CD, podemos calcular:
Respuesta
9
Ejercicio #5
Dado: trapecio isósceles.
Halla a
Solución en video
Solución Paso a Paso
Para responder a la pregunta, debemos conocer una regla importante de los trapecios isósceles:
La suma de los ángulos que delimitan cada uno de los lados trapezoidales (no las bases) es igual a 180
Por lo tanto:
∢B+∢D=180
3X+X=180
4X=180
X=45
Es importante recordar que esa aún no es la solución, porque nos pidieron el ángulo B,
Por lo tanto:
3*45 = 135
¡Y esta es la solución!
Respuesta
135°
Dado el polígono en el dibujo
¿Qué tipo es?
¿Los triángulos marcados son isósceles?
\( (ΔABE,ΔCED)\text{ } \)
Dado: \( ∢A=y+20 \)
\( ∢D=50 \)
trapecio isósceles.
Halla a \( ∢A \)
- Deltoide
- Paralelogramo
- Maneras de identificar paralelogramos
- Simetría rotacional en paralelogramos
- Del cuadrilátero al paralelogramo
- Trapecios
- Simetría en trapecios
- Área de un trapecio
- Perímetro de un trapecio
- Rectángulo
- De un cuadrilátero a un rectángulo
- Del paralelogramo al rectángulo
- Cuadrado
- El área de un cuadrado
- De paralelogramo a cuadrado
- Segmento medio
- Segmento medio de un trapecio
- Área
- ¿Rombo, cometa o diamante?
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
- El área de un rombo
- Perímetro
- Áreas de Polígonos para 7º Grado
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









