¡Desde ahora podrás determinar si el cuadrilátero frente a ti es un paralelogramo!
Te presentamos 5 formas diferentes de demostrarlo
Cuando:
¡Desde ahora podrás determinar si el cuadrilátero frente a ti es un paralelogramo!
Te presentamos 5 formas diferentes de demostrarlo

Cuando:
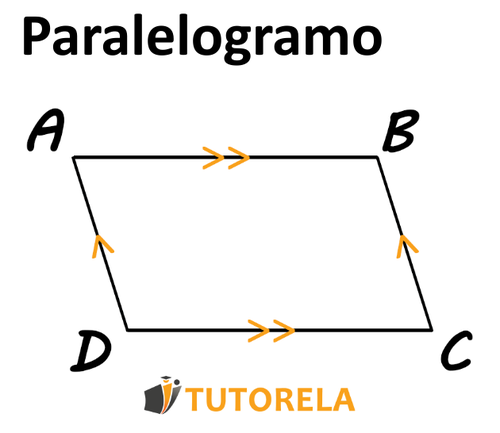
En un cuadrilátero donde cada par de lados opuestos también son paralelos entre sí, el cuadrilátero es paralelo.
Se nos pregunta, ¿cada par de lados en el cuadrilátero también es paralelo? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.

Cuando:
y también
Entonces:
Paralelogramo.
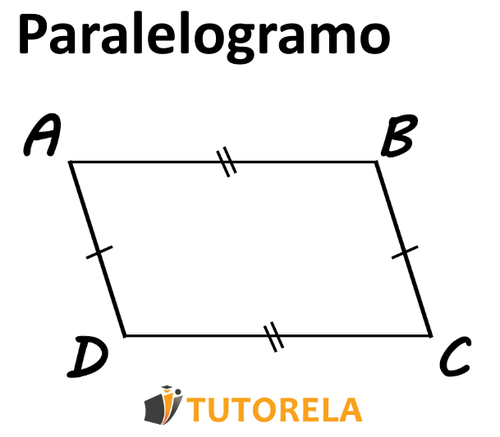
En un cuadrilátero donde cada par de lados opuestos también son iguales entre sí, el cuadrilátero es paralelo.
Se nos pregunta, ¿cada par de lados opuestos en el cuadrilátero también son iguales? Si la respuesta es sí, se determina que el cuadrilátero es paralelo.
Cuando:
Y también
Entonces:
Paralelogramo.
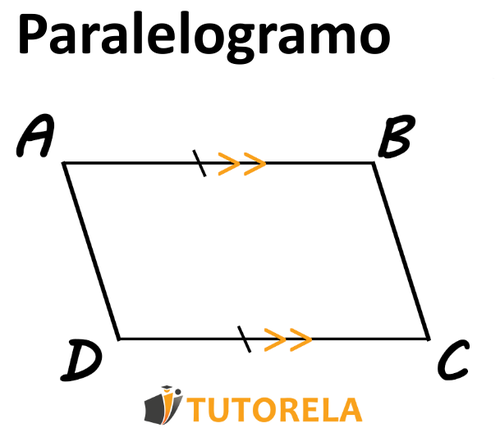
Si un cuadrilátero tiene un par de lados opuestos que son iguales y paralelos, el cuadrilátero es un paralelogramo.
Se nos pregunta, ¿hay un par de lados en el cuadrilátero que sean iguales y paralelos? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
Cuando:
y también
Entonces:
Paralelogramo.
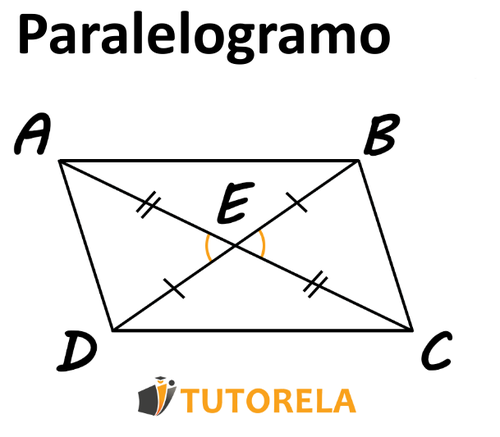
Si en un cuadrilátero, las diagonales se cortan, el cuadrilátero es un paralelogramo.
Se nos pregunta, ¿en este cuadrilátero se cortan las diagonales? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
Cuando:
y también
Entonces:
Paralelogramo.
Si un cuadrilátero tiene dos pares de ángulos opuestos iguales, el cuadrilátero es un paralelogramo.
Se nos pregunta, ¿hay dos pares de ángulos opuestos iguales en este cuadrilátero? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
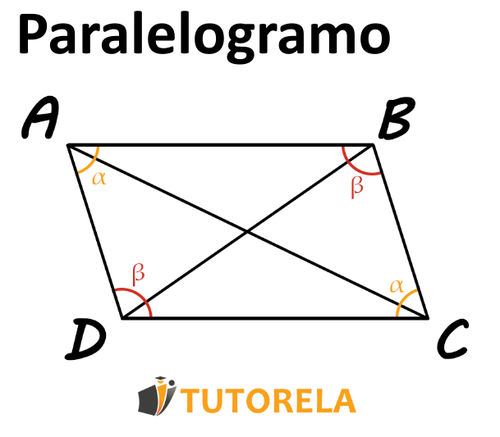
Cuando:
Entonces:
Paralelogramo.
Hace tiempo que conocemos el querido y familiar cuadrilátero, ¡pero hoy revelaremos cómo determinar que el cuadrilátero que tenemos frente a nosotros es en realidad un paralelogramo!
Primero recordaremos las características que conocemos sobre el cuadrilátero
Probablemente te estés preguntando, ¿qué hace que nuestro cuadrilátero sea un paralelogramo o cómo podemos determinar con certeza que un cuadrilátero es un paralelogramo?
No te preocupes, estamos aquí para enseñarte, aprenderemos algunas formas principales para ayudarte a determinar si tu cuadrilátero es también un paralelogramo.
La primera forma de determinar que un cuadrilátero es un paralelogramo es examinar la siguiente afirmación:

¿Cómo recordamos esto?
La palabra paralelogramo recuerda mucho a la palabra paralelo.
¡Así es como recordamos que estamos buscando lados que sean paralelos!
Tenga en cuenta: Este argumento tiene mucho sentido ya que la definición del paralelogramo es un cuadrilátero en el que cada par de lados opuestos es paralelo.
Se nos pregunta, ¿cada par de lados también están en un cuadrilátero? ¿Paralelos? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
La segunda forma de determinar que el cuadrilátero es un paralelogramo es examinar la siguiente afirmación:
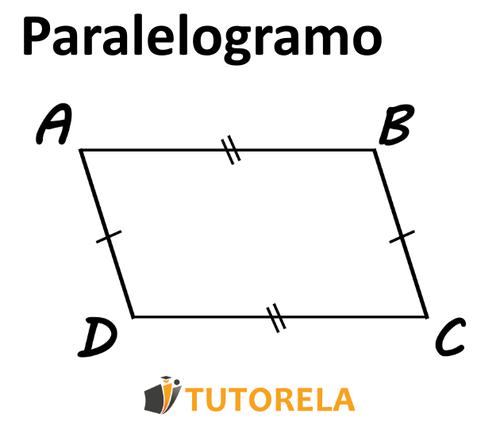
Nos preguntan, ¿cada par de lados opuestos en el cuadrilátero son iguales? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
Para que pueda comprender mejor por qué este argumento es cierto, le mostraremos cómo esta afirmación se sostiene como prueba:
Todo lo que necesitaremos para probar esta afirmación es trazar una línea diagonal en nuestro cuadrilátero y superponer los triángulos formados por nosotros según :
Dado:
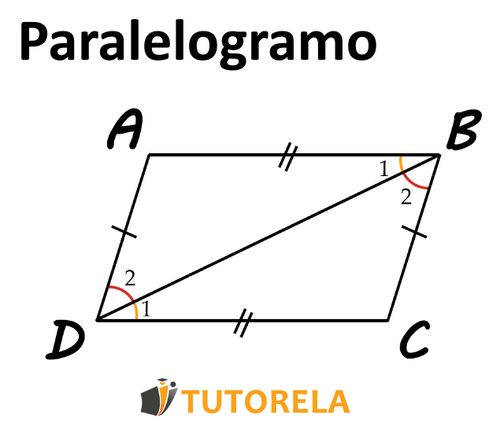
| Argumento | Explicación |
| Lado | Dado |
| Lado | Dado |
| Lado | Un lado común, cada tamaño igual a sí mismo. |
| Por lo tanto | Los triángulos se superponen según L.L.L |
| Se deduce que: | |
| Por la misma superposición | |
| Por la misma superposición | |
Alternos y también iguales | |
| Por lo tanto | Si los ángulos alternos son iguales, las rectas son paralelas |
Alternos y también iguales | |
| Y por lo tanto | Si los ángulos alternos son iguales, las rectas son paralelas |
| Se deduce que: ¡Es un paralelogramo! | Si cada par de lados opuestos en el cuadrilátero son paralelos entre sí, el cuadrilátero es un paralelogramo. |
La tercera forma de determinar que el cuadrilátero es un paralelogramo es examinar la siguiente afirmación:
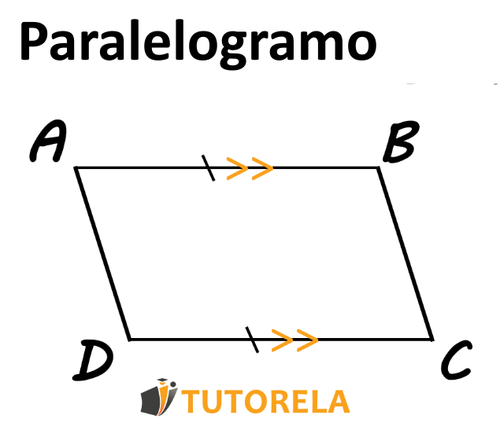
Tenga en cuenta: es suficiente un par de lados donde existen ambas propiedades: ambas paralelas e iguales y obtenemos un paralelogramo.
Se nos pregunta, ¿hay un par de lados en un cuadrilátero que sean iguales y también paralelos? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
Vamos a probar esta afirmación:
Primero trazaremos una diagonal en el cuadrilátero frente a nosotros
y podemos probar una superposición entre los dos triángulos creados para nosotros.
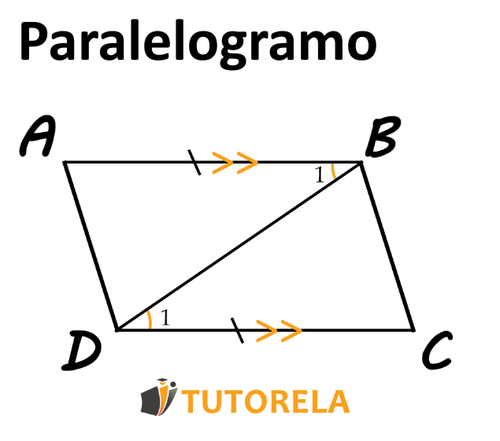
Dado que:
| Argumento | Explicación |
| Lado | Dado |
| Dado | |
| Se deduce que: Ángulo | Los ángulos alternos entre líneas paralelas son necesariamente iguales. |
| Lado | Un lado común, cada tamaño igual a sí mismo. |
| Y por lo tanto | Según L.A.L |
| Se deduce que: y también | Según superposición de ángulos |
| Se deduce que- ¡Es un paralelogramo! | Si cada par de lados opuestos en el cuadrilátero son paralelos entre sí, el cuadrilátero es un paralelogramo. |
La cuarta forma de determinar que el cuadrilátero es un paralelogramo es examinar la siguiente afirmación:
Presta atención: la condición habla de intersecciones diagonales y no solo de intersecciones.
¿Qué se entiende por diagonales que se intersecan entre sí?
Si una diagonal cruza a otra por la mitad - 2 mitades iguales y sucede lo mismo al contrario, las diagonales se cruzan entre sí.
Se nos pregunta, ¿las diagonales de este cuadrilátero se intersecan? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
Veamos esto en la figura:
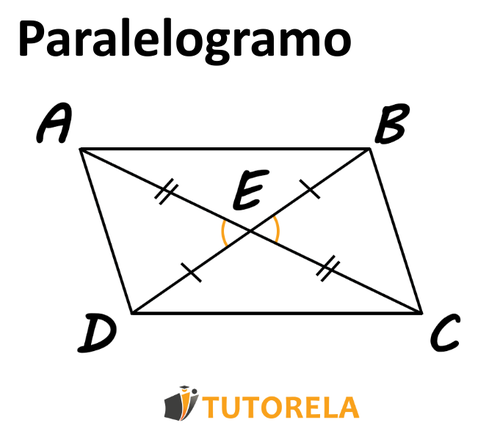
Podemos ver que en este cuadrilátero hay dos diagonales que se intersecan:
Vamos a probar esta afirmación:
Superpondremos entre y
según
| Argumento | Explicación |
| Lado | Dado |
| Ángulo | Los ángulos de los vértices son iguales entre sí. |
| Lado | Dado |
| Se deduce que: | Según L.A.L |
| Por lo tanto podemos decir que: Iguales y también alternos | Superposición de triángulos |
| Por lo tanto: | Si los ángulos alternos son iguales, las rectas son paralelas |
| Superposición de triángulos | |
| Y por lo tanto: ¡Es un paralelogramo! | Si un cuadrilátero tiene un par de lados opuestos que son iguales y paralelos, el cuadrilátero es un paralelogramo. |
La quinta forma de determinar que el cuadrilátero es un paralelogramo es examinar la siguiente afirmación:
Es decir:
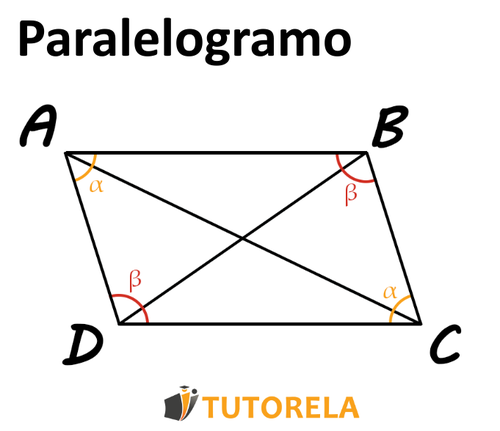
Si
Entonces el cuadrilátero frente a ti Es un paralelogramo.
Se nos pregunta, ¿hay dos pares de ángulos opuestos iguales en este cuadrilátero? Si la respuesta es sí, se determina que el cuadrilátero es un paralelogramo.
Para que entiendas mejor la lógica detrás de esta afirmación, lo probaremos aquí:
Alargaremos un poco los lados del cuadrilátero y obtendremos:
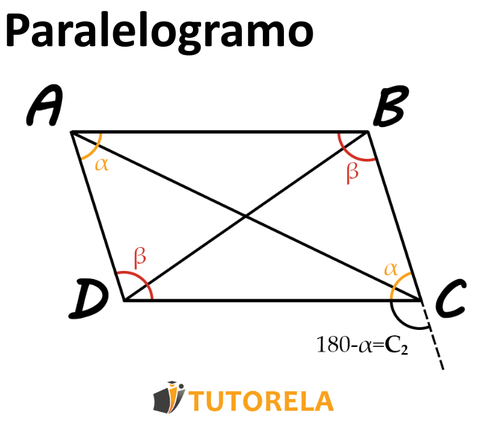
Es un ángulo adyacente a , se encuentra con él en la misma línea y por lo tanto complementa a .
Se determina que:
¿Qué más sabemos?
que la suma de los ángulos de un cuadrilátero es igual a .
Por lo tanto podemos determinar que:
Podemos aislar β y obtener:
Ahora notaremos que el ángulo y el ángulo Tiene el mismo tamaño: .
Tenga en cuenta que se nos pidió por los ángulos correspondientes.
Si los dos ángulos correspondientes también son iguales, entonces las dos rectas que los forman son paralelas.
Lo mismo podemos probar con el segundo par de ángulos correspondientes y probar el paralelismo del segundo par de lados en un cuadrilátero.
¡Maravilloso! Ahora conoces todas las formas de determinar si un cuadrilátero es también un paralelogramo.