Aprendimos en el artículo anterior sobre la recta numérica Y también hablamos de números positivos y negativos. En este artículo seguimos avanzando y los llamaremos números enteros.
Números enteros
¿Qué son los números enteros?
El término "número entero", se refiere a todo número, a la izquierda del cual aparece el signo de más (+), o el signo menos (-).
- El signo de más () nos indica que el número es positivo (mayor que cero). El signo de menos (-) significa que el número es negativo (menor que cero).
- Cuando aparece un número sin uno de estos dos signos, significa que el número es positivo.
- Excepción: El número . El cero es el único número que no es ni positivo ni negativo. Es posible escribir "" o "", pero en este caso los signos no tendrán ningún significado.
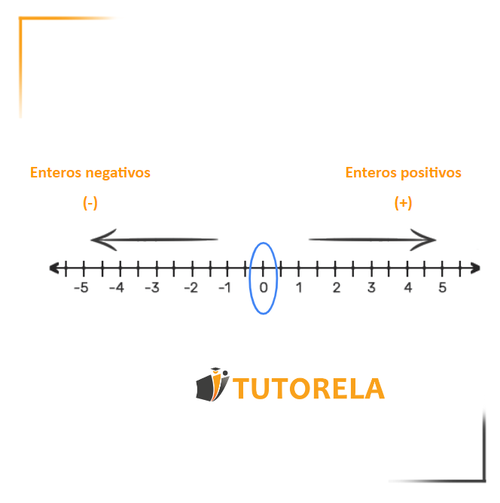
¡Pruébate en números dirigidos!
Cuál será el signo del resultado del siguiente ejercicio:
\( 5\cdot(-\frac{1}{2})= \)
Ejemplos:
Dependiendo de la ubicación de los números en la recta numérica, se pueden determinar las siguientes reglas:
- Un número positivo siempre es mayor que un número negativo.
- Si tenemos dos números positivos, el número cuyo valor absoluto es más grande, será el número mayor.
- Si tenemos dos números negativos, el número cuyo valor absoluto es más chico, será el número menor.
Ejercicios con números enteros
Ejercicio 1
Escribe en el espacio en blanco uno de los siguientes signos:
- __
- __
- __
- __
- __
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-4)\cdot12= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-6)\cdot5= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( 2\cdot(-2)= \)
Ejercicio 2
Lee las siguiente oraciones, y determina si cual es falsa o verdadera:
- Todo número positivo es mayor que cero.
- Se puede omitir el signo menos.
- El signo siempre se escribe a la izquierda del número.
- "" y "" son dos formas de escribir el mismo número.
- El número aparece en la recta numérica a la derecha del número .
- Todos los números negativos aparecen en la recta numérica a la izquierda del número .
- El número es más pequeño que el número .
Ejercicio 3
Consigna
¿Cuál es el valor que colocaremos para resolver la siguiente ecuación?
Solución
Para responder a esta pregunta es posible contestar de dos maneras:
Una forma es el reemplazo:
Colocamos potencia de y parece que hemos llegado al resultado correcto, es decir:
Otra forma es mediante la raíz
Es decir
Respuesta:
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-16)\cdot(-5)= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-3)\cdot(-4)= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-2)\cdot(-\frac{1}{2})= \)
Ejercicio 4
Consigna
¿Cuál es el resultado de la siguiente potencia?
Para resolver esta consigna primero debemos entender el significado del ejercicio
Ahora es todo más simple… ¿Correcto?
Obtenemos:
Respuesta
Ejercicio 5
Consigna
Solución
Presta atención que menos multiplicado por menos se convierte en más, y por lo tanto
Respuesta
¿Cuál será el signo del resultado del ejercicio siguiente?
\( \frac{1}{4}\cdot\frac{1}{2}= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( 6\cdot3= \)
¿Cuál será el signo del resultado del ejercicio?
\( (-14):(+8) \)
Ejercicio 6
Consigna
Solución
Primero resolvemos los puntos de multiplicación, es decir, los puntos que tienen un signo más o menos antes de otro signo.
Ahora resolvemos como un ejercicio común:
Respuesta
Ejercicio 7
Consigna
Dado que:
Número negativo
Número negativo
¿Cuál es la suma de ?
Solución
Cuando sumamos dos números negativos, el resultado que obtendremos será un número negativo.
Respuesta
Negativo
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Números positivos, negativos y el cero
Eliminación de paréntesis en números reales
Suma y resta de números reales
Multiplicación y división de números reales
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-2)\cdot(-4)= \)
¿Cuál será el signo del resultado del ejercicio?
\( (+3\frac{1}{4}):(+\frac{2}{5}) \)
¿Cuál será el signo del resultado del ejercicio?
\( (+7.5):(+3) \)
Preguntas de repaso
¿Qué son los números enteros y cuáles son?
Los números enteros los podemos escribir sin parte decimal y nunca con fracción, por ejemplo no son números enteros. Por lo tanto los números enteros son aquellos positivos, negativos (sin decimal) y el cero.
Por ejemplo:
es decir los números naturales con sus respectivos negativos.
¿Cómo contar números enteros?
Los enteros los podemos ubicar en la recta numérica de la siguiente manera:
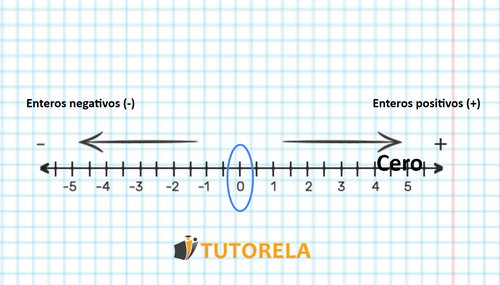
Existen reglas para poder contar los enteros, veamos el caso de la suma:
- Si sumamos dos números enteros positivos, solo sumamos los valores absolutos y conservamos el signo positivo.
Ejemplo 1
Los dos números son positivos y el resultado sigue siendo positivo.
- Al sumar números negativos se suman y el resultado sigue siendo negativo.
Ejemplo 2
Se suman los valores absolutos, pero el resultado sigue siendo negativo.
- Cuando tenemos números con diferente signo se restan, es decir, al número mayor le quitamos el número menor y el resultado tendrá el signo del número con mayor valor absoluto.
Complete el número faltante:
\( 10\cdot?=-100 \)
Complete el número faltante:
\( (-6)\cdot?=-12 \)
Cuál será el signo del resultado del siguiente ejercicio:
\( 5\cdot(-\frac{1}{2})= \)
Ejemplo 3
En esta operación podemos ver qué tenemos números con diferentes signos, por lo tanto se restan y pondremos el signo del número mayor, en este caso el resultado es negativo.
Aquí al número más grande le restamos el más chico y en este caso el resultado será positivo porque el número más grande tiene signo positivo.
¿Qué es un número entero para niños?
Un número entero es aquel que no tiene ningún decimal o es aquel que no lo podemos escribir como fracción.
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-4)\cdot12= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-6)\cdot5= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( 2\cdot(-2)= \)
¿Qué números no son enteros?
Los números decimales, racionales y los números irracionales no son números enteros, como por ejemplo:
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-16)\cdot(-5)= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-3)\cdot(-4)= \)
¿Cuál será el signo del resultado del ejercicio siguiente?
\( (-2)\cdot(-\frac{1}{2})= \)
ejemplos con soluciones para Números dirigidos
Ejercicio #1
Cuál será el signo del resultado del siguiente ejercicio:
Solución en video
Solución Paso a Paso
Recordemos la regla:
Por lo tanto, el signo del resultado del ejercicio será negativo:
Respuesta
Negativo
Ejercicio #2
¿Cuál será el signo del resultado del ejercicio siguiente?
Solución en video
Solución Paso a Paso
Recordemos la regla:
Por lo tanto, el signo del resultado del ejercicio será negativo:
Respuesta
Negativo
Ejercicio #3
¿Cuál será el signo del resultado del ejercicio siguiente?
Solución en video
Solución Paso a Paso
Para resolver el ejercicio necesitas recordar una regla importante: Multiplicar un número positivo por un número negativo da como resultado un número negativo.
Por lo tanto, si multiplicamos menos 2 por 2 el resultado será menos 4.
Es decir, el resultado es negativo.
Respuesta
Negativo
Ejercicio #4
¿Cuál será el signo del resultado del ejercicio siguiente?
Solución en video
Solución Paso a Paso
Recordemos la regla:
Por lo tanto, el signo del resultado del ejercicio será positivo:
Respuesta
Positivo
Ejercicio #5
¿Cuál será el signo del resultado del ejercicio siguiente?
Solución en video
Solución Paso a Paso
Recordemos la propiedad:
Por lo tanto, el signo del resultado del ejercicio será positivo:
Respuesta
Positivo
- Jerarquía de operaciones: suma, resta, multiplicación y división
- Jerarquía de operaciones: potencias
- Jerarquía de operaciones: (raíces)
- División y línea de fracción
- Los números 0 y 1 en las operaciones
- Elemento neutro / Elementos neutros
- Jerarquía de operaciones con paréntesis
- Inverso multiplicativo
- Orden o jerarquía de las operaciones con fracciones
- Operaciones aritméticas avanzadas: Resta de sumas, resta de diferencias, división por producto y división por cociente
- La propiedad conmutativa
- Propiedad conmutativa de la suma
- Propiedad conmutativa de la multiplicación
- La propiedad asociativa
- Propiedad asociativa de la suma
- Propiedad asociativa de la multiplicación
- Propiedad distributiva
- La propiedad distributiva para alumnos de 1.º de ESO
- La propiedad distributiva en el caso de las divisiones
- La propiedad distributiva en el caso de la multiplicación
- Resta de números enteros con paréntesis en los que hay sumas
- División de números enteros entre paréntesis en los que hay una división
- Resta de números enteros con paréntesis en los que hay restas
- División de números enteros entre paréntesis en los que hay una multiplicación
- Las propiedades conmutativas, la multiplicación, la propiedad distributiva y ¡otras más!
- Potencias y raíces
- ¿Qué es una raíz cuadrada?
- Raíz de número negativo
- Potencias y Propiedades de potenciación
- Potencias
- Base de una potencia
- El exponente de una potencia









