Factorización

Haremos uso de las fórmulas de multiplicación abreviada para convertir expresiones con términos que tienen entre ellos signos de sumar o de restar a expresiones cuyos términos se multiplican.

$a^2-b^2=(a-b)\cdot(a+b)$

$a^2+2ab+b^2=(a+b)^2$

$a^2-2ab+b^2=(a-b)^2$

Para utilizar la primera fórmula:
$a^2-b^2=(a-b)\cdot(a+b)$

Nos preguntaremos:

• ¿Hay una expresión positiva y otra negativa?
• ¿Podemos encontrar la raíz de cada una de las expresiones por separado?

Si hemos contestado afirmativamente a ambas preguntas, todo lo que nos queda por hacer es simplemente sacar la raíz de los dos términos y escribirlas según la fórmula.

Observa:

• Colocaremos las raíces entre los paréntesis.
• En caso de que llegara a haber dos términos positivos o dos términos negativos no será posible utilizar esta fórmula.

Para utilizar las otras fórmulas:
$a^2+2ab+b^2=(a+b)^2$

$a^2-2ab+b^2=(a-b)^2$

Deberemos corroborar que se cumplan tres condiciones.

Nos preguntaremos:

• ¿Los dos términos de los cuales sacaremos las raíces tienen el mismo signo? Es decir ¿ambos son positivos o ambos son negativos?
• ¿Podemos sacar la raíz de los dos términos por separado?$a$  y $b$ ?
• Si multiplicamos el producto de las raíces por $2$ ¿obtendremos el término medio (en positivo o en negativo)?

Si todas las respuestas son afirmativas, todo lo que nos queda por hacer es simplemente colocar las raíces obtenidas en la fórmula correspondiente. Observa que, si el término del medio era negativo en el ejercicio original, lo colocaremos en la fórmula con el signo de restar.

¿Cuándo no se pueden utilizar estas fórmulas?

Cuando en el ejercicio original los signos de los términos de los cuales queramos sacar raíces sean diferentes, es decir, uno positivo y otro negativo, no podremos utilizar estas fórmulas.

Podemos sacar de los paréntesis a un factor que sea común a ambos elementos y dejar dentro una expresión sencilla y cómoda.
El factor común es el mayor factor que es común a ambos elementos por completo.

Fíjate cuál es el mayor número libre que podemos extraer.

Luego pasemos a las incógnitas y preguntemos

¿cuál es la menor cantidad de veces que aparece la $X$ en algún elemento?

Multipliquemos el número libre por la incógnita la cantidad de veces que hemos encontrado y obtendremos el mayor factor común.

La extracción del factor común es la primera operación que intentamos llevar a cabo cuando necesitamos descomponer alguna expresión en factores.

Para corroborar que has extraído el factor común correctamente abre los paréntesis y observa si has llegado al ejercicio original.

Te presentamos al trinomio:
$ax^2+bx+c$

El trinomio representa una expresión en la cual la $X$ está elevada a la segunda potencia y la precede un coeficiente que puede ser positivo o negativo, pero nunca $0$ (a veces el coeficiente equivale a $1$ y, en esos casos no se vera la a), a este elemento puede agregarse o quitarse otro $bx$, donde la $b$ representa el coeficiente (bajo las mismas condiciones de la a) y se le puede adjuntar alguna variable independiente -número-> $c$. No importa si los coeficientes de las variables son positivos o negativos, siempre y cuando estén acorde al modelo del trinomio, el ejercicio se denominará trinomio.

La factorización se verá del siguiente modo:
 (x+solución\space uno)(x+solución\spacedos)

Buscaremos dos números cuyo producto sea $a\cdot c$ y su suma sea $b$

Nos preguntaremos: qué número multiplicado por qué otro nos dará $a\cdot c$  o $​​c$  (si $a$  equivale a $1$).
y qué más qué sumará $b$.

De hecho, tenemos que encontrar un par de números que cumplan con estas dos condiciones a la vez.

Podemos trazarlo del siguiente modo:

Modo de acción:
Encontraremos todos los números cuyos productos sean $A\cdot C$ y los anotaremos.
Luego, veremos qué par de números dentro de los que hallamos nos dará por resultado $B$.
Los dos números que cumplen con ambas condiciones son las soluciones del trinomio.

Importante:

• Si A fuese distinto de $1$ aparecería antes de los paréntesis y luego habría una multiplicación.
• Si alguna de las soluciones o ambas fuesen negativas no las sumaríamos a la $X$ sino las restaríamos.

$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$

$a$  El coeficiente del primer término
$b$  El coeficiente del segundo término
$c$  El número libre

En primer paso utilizaremos sólo la suma y hallaremos la primera solución y luego, utilizaremos sólo la resta y encontraremos la segunda.
Nuevamente, la factorización se verá del siguiente modo:
$(x+solución\space primero)(x+solución\space segundo)$
o con restas, según los resultados.

Las fracciones algebraicas son fracciones con incógnitas.
Modos de acción para factorizar fracciones algebraicas:

• Hallaremos el factor común más apropiado para extraer.
• Si no vemos un factor común que podamos extraer, pasaremos a la factorización con fórmulas de multiplicación abreviada, tal como lo hemos estudiado.
• Si no se pueden utilizar las fórmulas de multiplicación abreviada, pasaremos a factorizar con trinomios.
• Reduciremos acorde a las reglas de reducción (multiplicación de elementos).

Observa, puedes factorizar toda expresión incluida en tu fracción del modo que desees y, al final, llegarás a expresiones factorizadas.

Para sumar o restar fracciones algebraicas deberemos hacer que todos los denominadores sean iguales, es decir, llegar al común denominador.

Para hacerlo deberemos descomponer en factores según los diferentes modos que hemos aprendido.

Pasos de acción:

• Descompondremos en factores (factorizaremos) todos los denominadores que tenemos.
• Anotaremos el común denominador.
• Multiplicaremos cada uno de los numeradores por el mismo número que necesitemos multiplicar su denominador a fin de llegar al común denominador.
• Escribiremos el ejercicio con un solo denominador, el común denominador, y entre los numeradores conservaremos las mismas operaciones matemáticas que había en el ejercicio original.
• Luego de abrir los paréntesis puede ocurrir que nos topemos con otra expresión que haga falta factorizar. La descompondremos en factores y veremos si podemos simplificarla.
• Obtendremos una fracción común y la resolveremos.

Podrás simplificar fracciones algebraicas sólo cuando haya operaciones de multiplicación entre los elementos del numerador.
Observa que, si hay sumas o restas entre elementos encerrados entre paréntesis, sí podremos simplificar ya que éstos se consideran como un solo elemento.

En cualquier otro caso no se puede simplificar.
Luego de factorizar podrás simplificar muy fácilmente estas fracciones.
Pasos para simplificar fracciones:

• Observa el siguiente ejercicio e intenta entenderlo.
• Procura hallar el factor común.
• Trata de simplificar utilizando las fórmulas de multiplicación abreviada.
• Intenta factorizar con trinomios.

Pasos de acción para la multiplicación de fracciones algebraicas:

• Intentemos extraer el factor común.

Éste puede ser la incógnita o bien cualquier número libre.

• Si esto no alcanzara, factorizaremos con fórmulas de multiplicación abreviada y con trinomios.
• Encontremos el conjunto solución.

¿Cómo se halla el conjunto solución?
Haremos que todos los denominadores que tenemos equivalgan a $0$ y hallaremos la solución.
El conjunto solución será $X$: distinto de lo que causa que nuestro denominador equivalga a cero.

• Simplifiquemos las fracciones con seguridad.
• Multipliquemos numerador por numerador y denominador por denominador como en cualquier fracción.

Pasos de acción para la división de fracciones algebraicas:

• Convertiremos el ejercicio de dividir en uno de multiplicar como lo hacemos con las fracciones comunes.

¿Cómo lo haremos de forma correcta?

Dejaremos a la primera fracción tal como está, cambiaremos el signo de división por el de multiplicación y a la fracción que aparece después del signo la invertiremos. Es decir, numerador en lugar de denominador y denominador en lugar de numerador.

• Actuaremos acorde a las reglas de multiplicación de fracciones algebraicas:

1. Intentaremos extraer el factor común.

Éste puede ser la incógnita o bien cualquier número libre.

1. Si esto no alcanzara, factorizaremos con fórmulas de multiplicación abreviada o con trinomios.
2. Encontraremos el conjunto solución.

• ¿Cómo se halla el conjunto solución?

Haremos que todos los denominadores que tenemos equivalgan a $0$ y hallaremos la solución.

El conjunto solución será: $X$ distinto de lo que causa que nuestro denominador equivalga a cero.

• Simplifiquemos las fracciones con seguridad.
• Multipliquemos numerador por numerador y denominador por denominador como en cualquier fracción.

Resolución de ecuaciones por medio de la factorización
Recordemos la regla:

El producto de dos números equivale a $0$ cuando, por lo menos, uno de ellos vale $0$.

Si $x\cdot y=0$
entonces
o: $x=0$
o: $y=0$
o ambos valen $0$.
Pasos de acción para resolver ecuaciones por medio de la factorización:

1. Pasemos todos los elementos a un miembro de la ecuación y dejemos $0$ en el otro.
2. Factoricemos con alguno de los métodos que hemos aprendido: con la extracción del factor común, con fórmulas de multiplicación abreviada o con trinomios.
3. Veamos cuándo los elementos llegan a un producto equivalente a $0$.

La factorización es un método algebraico que aplicarás, de manera automática, en la mayoría de los ejercicios que recibirás de aquí en adelante.

La factorización nos permite representar y convertir términos entre los cuales hay sumas o restas a términos con operaciones de multiplicar o dividir.

Cuando se factoriza correctamente, el resultado no cambia, sólo que el ejercicio se ve representado de un modo diferente.

Claramente no estamos hablando sólo de modificaciones en las operaciones de suma y resta a las de multiplicación y división, sino de un cambio radical que aplica a todos los factores involucrados.

¿Por qué querríamos factorizar?

Puede ser que te estés preguntando para qué demonios querríamos convertir los términos con sumas y restas a otros con multiplicaciones y divisiones.

Si es así, es importante que sepas que, la factorización es la principal clave para lograr resolver ejercicios más complejos que los que has resuelto hasta hoy.

Luego de que leas todo lo que se explica aquí sabrás factorizar con total seguridad, de todas las maneras, con facilidad y rapidez.

De este modo, podrás resolver los ejercicios que recibas sin ningún problema.

Espera... ¿Cómo sabrás si te conviene factorizar?

Aquí enumeraremos los principales usos de la factorización.

1.Cuando te topes con ejercicios donde la suma o diferencia de sus términos dé cero, te convendrá aplicar la técnica de la factorización.

Al factorizar convertimos la suma y resta a operaciones de multiplicación y división.

Con la técnica de la factorización podemos convertir el total o la diferencia a un producto y, es sabido que, si el producto da $0$ quiere decir que al menos uno de los términos entre los cuales hay signos de multiplicar debe ser $0$

(ya que causa que el producto equivalga a cero).

Por ejemplo:

dado un ejercicio así:
$x^2+8x+15=$

Ejercicio que, en este momento, nos parece terrorífico y demasiado desafiante, podremos observarlo y entender que podemos aplicar la técnica de la factorización.

Todos los términos están en un miembro y en el segundo no hay nada, es decir $0$.

Entre los términos hay sumas.

Por lo tanto, con la técnica de factorización, que aprenderemos ahora mismo, podremos representar este ejercicio de la siguiente manera:
$(x+3)\cdot(x+5)=0$

Ya se ve mucho más sencillo ¿cierto?

Vemos que hay dos expresiones que su producto da $0$.

Podemos determinar que la primera expresión llega a cero y entonces $x=-3$
o que la segunda expresión llega a cero y entonces $x=-5$
o ambas. Por consiguiente, los resultados serán $x=-3,-5$

2.Cuando te topes con fracciones que tengan expresiones complicadas como las del ejemplo anterior, podrás llegar a fracciones mucho más sencillas con la factorización y simplificación correcta de los elementos.

Hemos dicho que, con ayuda de la factorización representamos el ejercicio que tiene operaciones de suma y resta como uno con operaciones de multiplicación y división, esto significa que no modificamos el ejercicio en sí, sólo su representación.

Entonces, podemos factorizar y simplificar el ejercicio de la manera que nos sea más cómoda para llegar al resultado correcto.

Por ejemplo, dado un ejercicio como éste:
$\frac{3X^2-14X+8}{3X^2+X-2}=$

A primera vista, parecería que no podemos simplificar el ejercicio y llegar a una fracción más simple ya que no podemos hacerlo cuando la expresión está compuesta de operaciones de suma y resta.

Pero ¡eh! Justamente para esto aprenderemos la técnica de la factorización.

Gracias a una sencilla factorización podremos obtener el mismo ejercicio, pero de la siguiente forma:

$\frac{(X-4)\cdot(X-\frac{2}{3})}{(X-\frac{2}{3})\cdot(X+1)}=$

¡Presta atención!

Ahora podemos simplificar el término fácilmente  $X-\frac{2}{3}$
Simplificaremos y obtendremos:

$\frac{X-4}{X+1}$

De una expresión bastante complicada, llegamos a una expresión sencilla aplicando la factorización.

Genial... Ahora que ya entiendes cuánto puede ayudarte la factorización en la resolución de ejercicios, seguro que ya debes tener curiosidad y querrás aprender las mejores técnicas para una factorización exitosa.

No te preocupes, exactamente para eso estamos aquí.

Te enseñaremos paso a paso todas las maneras para una factorización eficiente.

Comencemos con la primera.

Factorización según fórmulas de multiplicación abreviada

Seguramente te has topado alguna vez con las fórmulas de multiplicación abreviada.

Las fórmulas de multiplicación abreviada te ayudarán a convertir expresiones con términos que tenían entre ellos operaciones de multiplicación a expresiones cuyos términos se suman o restan.

Como lo hemos mencionado anteriormente, la factorización hace exactamente lo opuesto.

Convierte expresiones con términos que tienen entre ellos signos de sumar o de restar a expresiones cuyos términos se multiplican o dividen.

A consecuencia de esto, podremos utilizar las fórmulas de multiplicación abreviada que conocemos y rotarlas a favor de la factorización.

Comencemos por recordar las fórmulas de multiplicación abreviada:
$(a-b)\cdot(a+b)=a^2-b^2$

$(a+b)^2=a^2+2ab+b^2$

$(a-b)^2=a^2-2ab+b^2$

Las fórmulas nos ayudaron a abrir los paréntesis y ver las expresiones sin ellos.

Ahora aprenderemos cómo factorizar y volver a encerrar los términos dentro de los paréntesis.

Comencemos con la primera fórmula, esta vez giraremos las expresiones para que nos sea más cómodo entenderla:
$a^2-b^2=(a-b)\cdot(a+b)$

Como se puede ver, se trata de dos términos elevados a la potencia de dos, que tienen entre ellos una operación de restar.

De hecho, hablamos de un término positivo y otro negativo, ambos al cuadrado, cada uno por separado.

Veamos un ejemplo:
$x^2-16=$
¿Cómo sabremos si será posible resolver el ejercicio con la fórmula que vimos aquí arriba?

Nos preguntaremos:

• ¿Hay una expresión positiva y otra negativa? La respuesta es sí.
• ¿Podemos encontrar la raíz de cada una de las expresiones por separado? La respuesta es sí.

¡Perfecto! Ahora, todo lo que nos queda por hacer es simplemente sacar la raíz de estos dos términos.

Si sacamos la raíz del primer término obtendremos $X$.

Si sacamos la raíz del segundo término obtendremos $4$.

Ahora escribiremos las raíces que obtuvimos según la fórmula:
$x^2-16=(x-4)\cdot(x+4)$

Observa, acorde con la fórmula $B$ es $4$.

Ya que $16=4^2$

Entonces, de hecho, si vemos dos términos a los cuales podemos sacarle la raíz y uno es positivo y el otro negativo, podremos aplicar la primera fórmula de multiplicación con facilidad.

¡Atención! Observa el ejercicio muy atentamente y ubica las raíces dentro de los paréntesis. Si en el ejercicio anterior hubiéramos puesto el $16$ dentro de los paréntesis y no hubiéramos sacado la raíz, habríamos obtenido una respuesta errónea.

Y qué pasaría en caso de que hubiera un ejercicio así:
$-x^2+25$

Actuaremos con el mismo sistema:

• ¿Hay una expresión positiva y otra negativa? La respuesta es sí.
• ¿Podemos encontrar la raíz de cada una de las expresiones por separado? La respuesta es sí.

Por lo tanto, claramente que sí podremos aplicar la fórmula de multiplicación abreviada.

La operación de sumar entre los elementos no implica que no podamos utilizar esta fórmula.

El cambio en este ejercicio es solamente el orden en el que se escriben sus elementos.

Aun podemos captar que podemos sacar raíces del tercer y cuarto elemento.

Para no confundirnos daremos vuelta el ejercicio a su modo correcto y obtendremos:
$25-x^2=$
La factorización se verá así:
$(5-x)\cdot(5+x)$

Observa - En caso de que llegara a haber dos términos positivos o dos términos negativos no podremos utilizar esta fórmula.

Ahora pasaremos a las dos siguientes fórmulas de multiplicación abreviada y las giraremos para entenderlas mejor:

$a^2+2ab+b^2=(a+b)^2$

$a^2-2ab+b^2=(a-b)^2$

Aquellos con buen ojo probablemente noten que estas dos fórmulas son casi idénticas y, que la única diferencia entre ellas es el signo entre los elementos o el que precede al $2ab$.

Como podemos ver, se trata de dos términos $A$ y $B$ de los cuales se puede extraer raíz. Además, se añade o quita el producto de los elementos por $2$.

Veamos un ejemplo:
$x^2+12x+36=$

¿Cómo sabremos si será posible resolver el ejercicio con la fórmula que vimos aquí arriba?

Deberemos corroborar tres condiciones. Nos preguntaremos:

• ¿Los dos términos de los cuales sacaremos las raíces tienen el mismo signo? Es decir ¿ambos son positivos o ambos son negativos?

La respuesta es sí.
$36$ Positivo y $x^2$ positivo.

• ¿Podemos sacar la raíz de los dos términos por separado? $a$ y $b$ ?
  La respuesta es sí.
  Las raíces del término $a$ son $x$

y la raíz de $b$ es $6$.

• ¿El producto de las raíces por $2$ da el término medio (en positivo o en negativo)?

La respuesta es sí.

Si multiplicamos el término $a$

por el término $b$ y $2$,

obtendremos el término medio:
$x\cdot6\cdot2=12x$

¡Perfecto! Ahora, todo lo que nos queda por hacer es simplemente colocar las raíces obtenidas en la fórmula correspondiente:
$(x+6)^2$
Observa, si el término medio fuera negativo en el ejercicio, es decir:
$x^2-12x+36=$
habríamos utilizado la otra fórmula y la factorización se vería del siguiente modo:
$(x-6)^2$

Veamos un ejemplo del uso de la fórmula con signo de restar:
$x^2-6x+9$
Nuevamente, deberemos corroborar que se cumplan tres condiciones. Nos preguntaremos:

• ¿Los dos términos de los cuales sacaremos las raíces tienen el mismo signo? La respuesta es sí. Ambos son positivos.
• ¿Podemos sacar la raíz de los dos términos por separado? ¿$A$ y $B$? La respuesta es sí.

La raíz del término $A$ es $X$ y la raíz del término $B$ es $3$.

• ¿El producto de las raíces por $2$ da el término medio (en positivo o en negativo)? La respuesta es sí.

Si multiplicamos el término $A$ por el término $B$ y por $2$ obtendremos el término medio:
$x\cdot3\cdot2=6x$

Observa, el término medio en el ejercicio original es $-6x$ y nosotros hemos obtenido $6x$.

Por lo tanto, utilizaremos la fórmula con el signo de restar y obtendremos:
$(x-3)^2$

¿Cuándo no se pueden utilizar estas fórmulas?

Cuando en el ejercicio original los signos de los términos de los cuales queramos sacar raíces sean diferentes, es decir, uno positivo y otro negativo, no podremos utilizar estas fórmulas.

Factorización sacando el término común fuera de los paréntesis

A veces, podremos sacar de los paréntesis a un factor que sea común a ambos elementos y dejar dentro una expresión sencilla y cómoda.

¿Qué quiere decir factor común?

El factor común es el mayor factor que es común a ambos elementos por completo.

Por ejemplo en el siguiente ejercicio:
$3x+21=$
Separando cada elemento del ejercicio obtendremos :
$3\cdot x+3\cdot7=$
Veremos que el factor común a ambas expresiones es $-3$.
Por lo tanto, del siguiente modo podremos extraerlo de la expresión haciendo uso de los paréntesis, y obtendremos exactamente la misma expresión vista de otra manera:
$3(x+7)$
Si abrimos los paréntesis obtendremos claramente:
$3x+21=$

Lo que hemos hecho es quitar el mayor factor común a ambos elementos. De $3x$ sacamos $3$

y ha quedado$x$ y de $21$ sacamos $3$ y ha quedado $7$.

Podremos extraer cualquier factor como factor común, incluso incógnitas e incógnitas con coeficientes.

Veámoslo en el siguiente ejercicio:
$4x^2+8x=$
Al desarmar la expresión obtendremos:
$4\cdot x\cdot x+8\cdot x=$
El mayor factor común que podremos extraer es $4x$
Nos quedaremos con:
$4x(x+2)=$
Cuanto más practiques el modo de extraer el factor común, más intuitivo te resultará éste.
Sugerencia nuestra:

En primer lugar, encuentra el mayor número libre que puedas extraer.

En el ejemplo anterior, observemos los números libres y preguntemos, ¿cuál es el mayor factor por el cual se dividen sin problema el $4$ y el $8$?

La respuesta es $4$.

Luego, pasaremos a las incógnitas y preguntaremos ¿cuál es la mínima cantidad de veces que aparece la $X$ en un elemento en particular?

La respuesta es una vez.

Entonces podremos extraer $4\cdot X$ .
¿Cuándo hace falta extraer el factor común?
Repitamos, como en el principio de factorización con las fórmulas de multiplicación abreviada, la extracción del factor común nos ayuda a factorizar y a resolver el ejercicio de manera correcta y eficiente.

En los casos en que exista una diferencia o total equivalente a $0$, podremos convertir el ejercicio a un producto y examinar cuándo los factores llegan a cero.

Asimismo, en fracciones, podremos extraer un factor común y así reducir fácilmente la fracción.

Veamos un ejemplo:
$x^3-x^2=0$
Querremos extraer el factor común.

Nos preguntaremos ¿Cuál es el mayor factor común que podemos sacar de los dos términos? La respuesta es $x^2$

si sacamos $x^2$ de $x^3$ , nos quedará $x$ y si sacamos $x^2$ de $-x^2$ nos quedaremos con $-1$ .
Por consiguiente, la expresión se verá así:
$x^2 (x-1)=0$

Ahora, podemos resolverlo fácilmente.

Nos preguntaremos ¿Cuándo la expresión vale cero?

Ya que aquí hay factores o $x^2$ equivale a $0$ o $(x-1)$  equivale a $0$.
Resolveremos y obtendremos:
Caso 1:

$​​​​​​​x^2=0$
$x=0$
Caso 2:
$​​​​​​​x-1=0$
$x=1$

Por lo tanto, los resultados serán:
$x=0,-1$

¿Deseas corroborar que hayas sacado el factor común de forma correcta?

No hay problema. Simplemente abre los paréntesis y observa si llegas al ejercicio original.

Si la respuesta es sí, quiere decir que has extraído el factor común de forma correcta. Si no, te has equivocado y deberás volver a intentarlo.

Factorización de trinomios

No te asustes del término trinomio. Concíbelo como una herramienta de asistencia que podrás utilizar para descomponer tu ejercicio en factores.

Te presentamos el trinomio:
$ax^2+bx+c$

El trinomio representa un ejercicio en el cual la $x$ se eleva al cuadrado, la precede un coeficiente, positivo o negativo, pero nunca $0$ (a veces el coeficiente equivale a $1$ y por lo tanto no veremos la $a$,) a dicho término puede venir añadido o quitado algún otro $bx$, cuando $b$ representa el coeficiente (en las mismas condiciones que $a$) y se le agrega o quita la variable independiente - número $c$ que no es $0$.

De hecho, el trinomio podría verse del siguiente modo: $ax^2-bx-c$

Mas allá de que los coeficientes de los términos sean positivos o negativos, siempre que aparezcan a estilo de trinomio, el ejercicio se denominará «trinomio».

Modelo del trinomio:

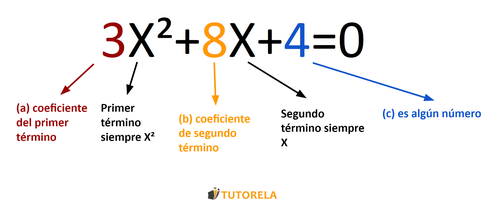
La factorización se verá así:
$(x+Solución \space Primero)(x+Solución\space Segundo)$
o con restas, según los resultados.

Veamos un ejemplo e intentemos entender exactamente los valores de estos parámetros: $x^2+4x+5=$

$a$  El coeficiente del primer elemento es $1$. Observa, no es $0$. A pesar de que no lo ves, existe y es el $1$. Si hubiese sido $0$, el primer término también se habría convertido en cero. En cambio, al multiplicar por $1$ no se modifica el término.
$b$  El coeficiente del segundo elemento es $4$.
$c$  El número libre es $5$.

Ahora aprenderemos cómo se factoriza con trinomios. Te enseñaremos dos maneras principales.

Atención: te recomendamos hacerlo de esta manera sólo cuando el coeficiente de $a$ equivalga a $1$.

Al observar nuestro trinomio, intentaremos encontrar dos números cuyo producto sea $a\cdot c$  y su suma sea $b$.
De hecho, preguntaremos: qué número multiplicado por qué otro nos dará $ac$ o $c$ (si $a$ equivale a $1$)
(y, qué número más qué otro sumará $b$.
De hecho, tenemos que encontrar un par de números que cumpla con estas dos condiciones a la vez.
Podemos trazarlo del siguiente modo:

Primeramente, encontraremos todos los números cuyos productos sean $AC$ y los anotaremos.

Luego, veremos qué par de números sumados nos darán $B$ como resultado.

Los dos números que cumplan con ambas condiciones serán las soluciones del trinomio.

Veamos un ejemplo:

$x^2+7x+6=$

Primero nos preguntaremos,

¿qué número multiplicado por qué otro nos dará $6$?

$6, 1$
$2,3$

Notemos que, aunque dichos números fueran negativos su producto sería $6$ (ya que menos multiplicado por menos da más).

Por consiguiente también añadiremos:
$1-, 6-$
$​​$,$​​-3,-2$

y luego, preguntaremos ¿la suma de qué par de números nos dará $7$?

La respuesta es: $6, 1$

Entonces la factorización del trinomio será: $x^2+7x+6=(x+1)\cdot(x+6)$

Observa, si $a$ difiriera de $1$ aparecería antes de los paréntesis y luego habría una multiplicación.

Sugerencia:
La primera manera es más oportuna para casos en los cuales el coeficiente del primer elemento $a$ equivale a $1$.
Entonces podremos preguntar cuáles son los dos números cuyo producto $c$ y su suma sea $b$.

Si $a$ difiere de $1$, preferiremos factorizar de la segunda manera.

Nota: Si alguna de las soluciones o ambas fuesen negativas no las sumaríamos a la $X$ sino las restaríamos.

Por ejemplo:
$x^2-7x+6=(x-1)\cdot(x-6)$

¿Deseas corroborar que has factorizado correctamente? Puedes abrir los paréntesis y ver si llegas al ejercicio original.

Si no eres del tipo de ensayo y error, y prefieres llegar a una respuesta concreta incluso cuando $a$ difiere de $1$  es conveniente que conozcas la fórmula cuadrática.

La fórmula cuadrática:

$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$

Sabemos que podría causar algo de miedo a primera vista, pero créenos, sólo tienes que saber identificar los elementos en tu ejercicio original y sustituirlos en la fórmula.

Además, probablemente te preguntes qué significan el más y el menos juntos.

La respuesta es simple.

Una vez sólo utilizaremos el más y encontraremos la primera solución y otra vez usaremos sólo el menos y encontraremos la segunda solución.

La fórmula cuadrática nos ayudará a resolver cualquier ecuación cuadrática.

Resolvamos el trinomio con esta fórmula.

Tomemos, por ejemplo, el trinomio:
$​​​​​​​x^2-8x+15=$

Primer paso:

Anotaremos los valores de todos los parámetros tal como lo hemos aprendido:
$a=1$
$b=-8$
$c=15$

Ahora, simplemente los colocaremos en la fórmula:
$=\frac{-(-8)±\sqrt{(-8^2)-4\cdot1\cdot15}}{2\cdot1}$

La primera vez solucionaremos sólo con el signo más:

$=\frac{-(-8)+\sqrt{(-8^2)-4\cdot1\cdot15}}{2\cdot1}$

$=\frac{8+\sqrt{64-60}}{2}$

$=\frac{8+\sqrt{4}}{2}$

$=\frac{8+2}{2}=\frac{10}{2}=5$

$5$ es nuestro primer resultado.

Ahora pasaremos a la fórmula con el signo menos:
$=\frac{-(-8)-\sqrt{(-8^2)-4\cdot1\cdot15}}{2\cdot1}$

Observa que podemos copiar todo lo que nos dio dentro de la raíz y simplemente cambiar el signo más por el de menos del siguiente modo:
$=\frac{8-\sqrt{4}}{2}$
$=\frac{8-2}{2}=\frac{6}{2}=3$

Nuestro segundo resultado es $3$.

Por lo tanto, $x^2-8x+15=(x+5)\cdot(x+3)$

Practica una y otra vez ambas maneras para saber cómo descomponer en factores con trinomios correcta y eficientemente.

Ahora, aprenderemos cómo descomponer fracciones algebraicas en factores.

Factorización de fracciones algebraicas

Entonces ¿qué son las fracciones algebraicas?

Las fracciones algebraicas son fracciones con incógnitas.

De hecho, todo lo que hemos estudiado sobre la factorización también tiene sentido en la factorización de fracciones algebraicas.

Cuando queramos descomponer factores algebraicos, actuaremos de las siguientes maneras:

1. Hallaremos el factor común más adecuado que nos convenga extraer.

¿Qué significa eso?

La clave en las fracciones algebraicas es que deben simplificarse, por eso, a veces buscaremos el factor común que nos convenga extraer para reducir la fracción.

2. Si no vemos un factor común que podamos extraer, pasaremos a la factorización con fórmulas de multiplicación abreviada, tal como lo hemos estudiado.

Las fórmulas de multiplicación abreviada también nos separan la expresión en factores y nos ayudan a reducir la fracción.

3. Si no se pueden utilizar las fórmulas de multiplicación abreviada, pasaremos a factorizar con trinomios.

¡Presta atención! Puedes factorizar toda expresión incluida en tu fracción del modo que desees y, al final, llegarás a expresiones factorizadas.

Veamos un ejemplo en el cual utilizaremos varios métodos de factorización de fracciones algebraicas:

$\frac{x^2-8x+16}{x^2-4x}=$

Notaremos que podemos factorizar el numerador a través de un trinomio y el denominador extrayendo un factor común simple.

Obtendremos:
$\frac{(x-4)(x-4)}{x(x-4)}=$
Ahora podemos reducir la expresión y obtener:
$\frac{x-4}{x}$

De hecho, hemos factorizado cada expresión de la manera más adecuada para nosotros.

¿En qué otros casos nos sirve la factorización? Cuando queremos sumar y restar fracciones algebraicas.

Suma y resta de fracciones algebraicas

Para sumar o restar fracciones algebraicas hay que causar que todos los denominadores sean iguales, es decir, llegar al común denominador.

Para hacerlo deberemos factorizar.

Pasos de acción:

1. Descompondremos en factores (factorizaremos) todos los denominadores que tenemos.
2. Anotaremos el común denominador.
3. Multiplicaremos cada numerador por el número necesario para llegar al común denominador.
4. Escribiremos el ejercicio con un solo denominador, el común denominador y, entre las expresiones de los numeradores, conservaremos las mismas operaciones matemáticas.
5. Resolveremos la fracción.

Veamos un ejemplo:

$\frac{x}{x+2}+\frac{3}{x+5}+\frac{6}{x^2+7x+10}=$

Tenemos un ejercicio con suma de varias expresiones. Para sumar estas fracciones deberemos causar que tengan un común denominador.

¿Cómo se encuentra el común denominador de todas las fracciones?

Factorizaremos el denominador de cada fracción por separado acorde a las distintas maneras que hemos aprendido.

Veamos que, en este ejercicio, sólo necesitaremos factorizar el denominador del tercer elemento. Lo haremos con un trinomio.

Y obtendremos:
$\frac{x}{x+2}+\frac{3}{x+5}+\frac{6}{(x+2)(x+5)}=$

El denominador común es $(x+2)(x+5)$. Por eso, trazaremos una raya fraccionaria y lo escribiremos:

Ahora, debemos multiplicar cada numerador por lo que necesita para llegar al común denominador:

Lo ilustraremos del siguiente modo para que puedas verlo con claridad:

Obtendremos:
$\frac{x(x+5)+3(x+2)+6}{(x+2)(x+5)}=$

Cuidaremos de conservar las operaciones matemáticas que hay entre los numeradores.

Abriremos paréntesis (sin tocar al común denominador) y obtendremos:
$\frac{x^2+5x+3x+6+6}{(x+2)(x+5)}=$
Colocaremos los elementos y nos dará:
$\frac{x^2+8x+12}{(x+2)(x+5)}=$
¡Presta atención! Tenemos un trinomio en el numerador.

Suerte que ya sabemos cómo descomponerlo en factores.

Factoricemos, nos dará:
$\frac{(x+5)(x+6)}{(x+2)(x+5)}=$

Oh... Ahora podemos reducir la expresión $x+2$

Lo haremos y obtendremos:
$\frac{x+6}{x+5}$
¡Éste es el resultado final!

Simplificación de fracciones algebraicas

La simplificación de fracciones algebraicas básicamente resume todo lo que hemos aprendido hasta ahora sobre la factorización.

Para simplificar fracciones algebraicas de manera eficaz y correcta, necesitarás conocer todas las maneras de factorización.

Desde la extracción del factor común, a través de las fórmulas de multiplicación abreviada y hasta la factorización de trinomios.

Observa:

Podrás simplificar fracciones algebraicas sólo cuando haya operaciones de multiplicación entre los elementos del numerador.

Sin embargo, si hay operaciones de suma o resta en elementos ubicados entre paréntesis, también podremos simplificar ya que éstos se consideran un solo elemento.

En cualquier otro caso no se puede simplificar.

Como ya hemos mencionado, la factorización es la manera para convertir un ejercicio con suma o resta a uno con multiplicación.

Luego de factorizar podrás simplificar muy fácilmente estas fracciones.

Pasos para simplificar fracciones:

Observa el siguiente ejercicio e intenta entenderlo.

1. Procura hallar el factor común.
2. Trata de simplificar utilizando las fórmulas de multiplicación abreviada.
3. Intenta factorizar con trinomios.

En algunos casos, podrías toparte con una fracción que tenga signos opuestos en el numerador y denominador.

Por ejemplo:
$\frac{2x-1}{1-2x}$

Observa que no puedes simplificar la expresión porque no hay operación de multiplicación entre los elementos (y también porque los signos son diferentes).

Para reducir esta fracción deberemos sacar $-1$ en el denominador o en el numerador y luego obtendremos la misma expresión en el denominador y en el numerador y podremos simplificar.

Saquemos $-1$ en el numerador y nos dará:
$\frac{(-1)(-2x+1)}{(1-2x)}=$

Observa que de hecho hemos recibido la misma expresión en el denominador y en el numerador y podremos quedarnos sólo con $-1$.

También podemos escribir:

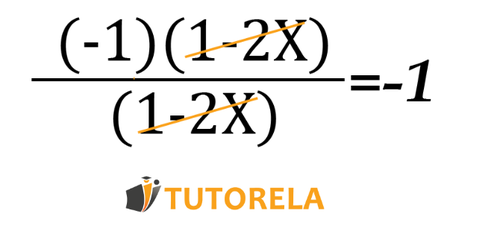
Y así ver mejor la simplificación. Observa que no hemos modificado los signos antes de los números.
$1$

Todavía positivo y $-2x$ todavía negativo.

Multiplicación y división de fracciones algebraicas

La multiplicación y división de fracciones algebraicas es muy similar a la multiplicación y división de fracciones comunes, por lo que no tienes por qué estresarte.

La única diferencia entre las fracciones algebraicas y las comunes es que primero tendremos que factorizar las expresiones dadas.

Además, ya que se trata de incógnitas, deberemos hallar el conjunto solución.

Luego de hacerlo, podremos simplificar y descubrir el numerador y la multiplicación.

En primer lugar, intentemos hallar el factor común. El factor común puede ser nuestra incógnita o cualquier número libre.

Si la extracción del factor común no fuera suficiente, factorizaremos con las fórmulas de multiplicación abreviada y también con el trinomio.

Luego hallaremos el conjunto solución.

¿Cómo se encuentra el conjunto solución?

Observemos nuestros denominadores y preguntémonos cuándo llegan a cero.

Es decir, hagámoslos equivalentes a $0$ y encontremos las soluciones.

El conjunto solución será: $X$ diferente de lo que causa que el denominador llegue a cero.

Luego, podremos reducir con seguridad las fracciones y multiplicar numerador por numerador y denominador por denominador como en cualquier fracción común.

Veamos un ejemplo:

$\frac{2x+4}{3x^2-3x}\cdot\frac{x-1}{4x^2+8x}=$

Factoricemos cada expresión a través de las maneras que hemos aprendido:
$\frac{2(x+2)}{3x(x-1)}\cdot\frac{x-1}{4x(x+2)}=$

Encontremos el conjunto solución:

$3x(x-1)=0$
$x≠0,1$
$4x(x+2)=0$
$x≠0, -2$
Por lo tanto, el conjunto solución es:
$x≠0,1, -2$ Ahora, podemos reducir las fracciones con seguridad.
Reduciremos y obtendremos:

$\frac{2}{3x}\cdot\frac{1}{4x}=$
Multipliquemos numerador por numerador, denominador por denominador y obtendremos:

$\frac{2}{12x^2}=\frac{1}{6x^2}$

Ahora pasemos a la división de fracciones algebraicas.

División de fracciones algebraicas

Cuando tengamos una división de fracciones algebraicas, primeramente convertiremos el ejercicio de dividir en uno de multiplicar como lo hacemos con las fracciones comunes.

¿Cómo lo haremos de forma correcta?

Dejaremos a la primera fracción tal como está, cambiaremos el signo de división por el de multiplicación e invertiremos la fracción que aparece después del signo. Es decir, el numerador pasa al lugar del denominador y viceversa.

Luego, cuando el ejercicio ya pase a ser un ejercicio con multiplicación, lo resolveremos exactamente como hemos estudiado antes. Primero intentaremos factorizar extrayendo el factor común, con las fórmulas de multiplicación abreviada y con trinomio,

hallaremos el conjunto solución, reduciremos y multiplicaremos numerador por numerador y denominador por denominador.

Veamos un ejemplo:
$\frac{x^2-10x+25}{x^2+2x}:\frac{x^2-25}{x+2}=$

Incluso antes de mirar el ejercicio convirtámoslo en un ejercicio de multiplicar. Dejaremos a la primera fracción tal como está, cambiaremos el signo de división por el de multiplicación e invertiremos la segunda fracción.

Lo haremos y obtendremos:
$\frac{x^2-10x+25}{x^2+2x}\cdot\frac{x+2}{x^2-25}=$

Genial. Ahora actuaremos acorde a las reglas de multiplicación de fracciones algebraicas.

Factoricemos de todas las maneras que sabemos:

$\frac{(x-5)(x-5)}{x(x+2)}\cdot\frac{x+2}{(x-5)(x+5)}=$

Encontremos los conjuntos solución:
$x≠0,-2,5,-5$
Reduzcamos las fracciones:

Obtendremos:

$\frac{x-5}{x}\cdot\frac{1}{x+5}$

Multipliquemos numerador por numerador y denominador por denominador, obtendremos:
$\frac{x-5}{x(x+5)}$

Resolución de ecuaciones por medio de la factorización

Podemos resolver ecuaciones descomponiendo factores fácil y rápidamente si actuamos siguiendo estrictamente los pasos adecuados.

La clave yace en conocer todas las maneras para factorizar exitosamente y, por supuesto, en entender una regla matemática básica.

La regla de la que estamos hablando es que el producto de dos términos equivale a cero si al menos uno de los términos es igual a $0$.

Es decir, dada la ecuación $x\cdot y=0$
La ecuación será consistente sólo si, al menos, uno de sus términos es $0$.

O bien:
$x=0$   o: $y=0$

Excelente. Una vez mencionada esta regla, continuemos con el orden de operaciones deseado para la resolución de ecuaciones con la factorización.

Cuando te topes con una ecuación, primero tendrás que pasar todos los elementos a un solo miembro y dejar $0$ en el otro.

Por ejemplo, si tienes una ecuación de este tipo:
$x^2+8x=-2x$

Deberás traspasar miembros para dejar sólo el $0$ en uno de ellos.

Traspasemos miembros y obtendremos: $x^2+8x+2x=0$

Ahora nos queda más claro que la factorización será muy efectiva en una ecuación como ésta.

Ya que, en la factorización, lo que en realidad hacemos es convertir una expresión que tiene sumas o restas a otra con operaciones de multiplicación y, como ya hemos mencionado, cuando los elementos se multiplican y su producto es $0$, será muy fácil encontrar las soluciones.

Entonces, luego de traspasar miembros y dejar el $0$ en uno de ellos, intentaremos factorizar la ecuación extrayendo el factor común, fórmulas de multiplicación abreviada o trinomio.

Colocaremos elementos en la ecuación del ejemplo anterior y obtendremos:

$x^2+10x=0$
Ahora, saquemos el factor común y nos dará:
$x(x+10)=0$
Nos preguntaremos ¿cuándo la ecuación da cero?

Las respuestas obviamente son:

cuando $x=0,-10$
éstas son nuestras soluciones.

Ahora que ya sabes todo acerca de la factorización, todas las formas de hacerla y sus usos, podrás practicar una y otra vez todos los métodos y ¡llegar muy feliz al examen con una excelente preparación!

Si te interesa este artículo también te pueden interesar los siguientes artículos:

• Factorización
• Los usos de la factorización
• Factorización según fórmulas de multiplicación abreviada
• Factorización a través de la extracción del factor común fuera de los paréntesis
• Factorización de trinomios
• Factorización de fracciones algebraicas
• Suma y resta de fracciones algebraicas
• Simplificación de fracciones algebraicas
• Multiplicación y división de fracciones algebraicas
• Resolución de ecuaciones por medio de la factorización

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.