Fórmula para calcular el área del triángulo escaleno:
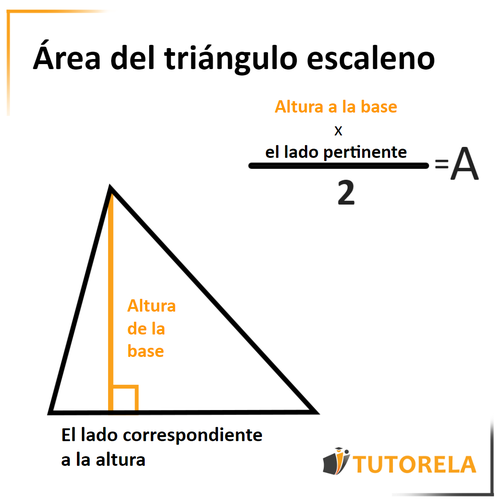
Fórmula para calcular el área del triángulo escaleno:

Completa la oración
Para encontrar el área de un triángulo rectángulo, se debe multiplicar a _ entre sí y dividir por 2.
Es muy sencillo calcular el área del triángulo escaleno si recordamos la fórmula y llevamos a cabo los pasos estrictamente. No te preocupes, estamos aquí para enseñarte exactamente a qué prestarle atención ¡no te dejaremos a la deriva!
Antes que nada, veamos la fórmula que debes recordar a fin de calcular el área del triángulo escaleno:

Se multiplica la altura por la base (el lado correspondiente a dicha altura) y se divide por .
Pon atención:
Corrobora colocar en la fórmula la altura y el lado correspondientes. Es decir, si se coloca en la fórmula una cierta altura y un lado que no es el que forma un ángulo de grados con la altura utilizada será erróneo.
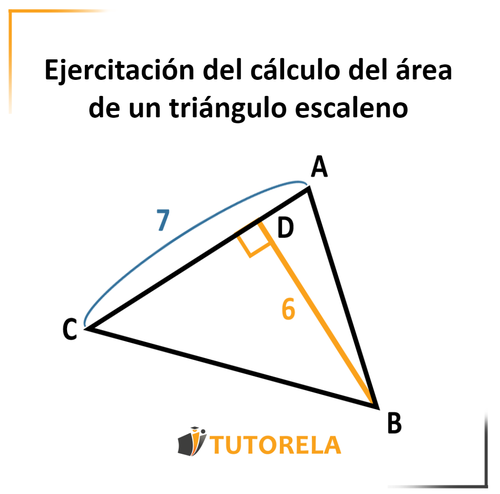
Dado el triángulo
Dado que:
Altura
¿Cuál es el área del triángulo?
Solución:
Veremos que el lado dado realmente es el que forma, con la altura, un ángulo de grados.
Después de corroborar el dato nos dirigiremos a la fórmula y colocaremos allí:
El área del triángulo es
Calcula el área del triángulo siguiente:
Calcula el área del triángulo siguiente:
Halla el área del triángulo mediante los datos de la figura:
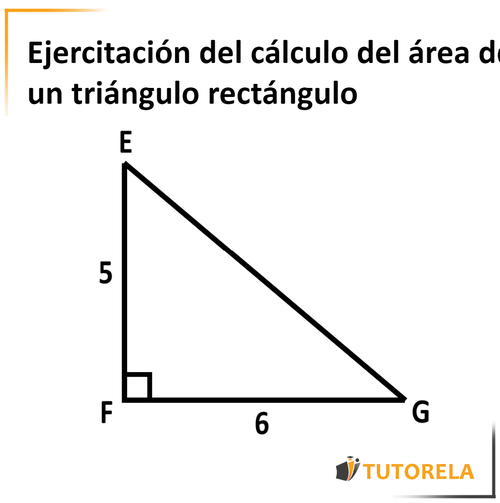
Dado el triángulo rectángulo
Dado que:
ángulo
Calcula el área del triángulo.
Solución:
Recordemos que la clave para calcular el área de cualquier triángulo es multiplicar la altura
por el lado correspondiente y luego dividir dicho producto por
En un triángulo rectángulo, en realidad, ¡ya tenemos la altura!
No tenemos la necesidad de calcular otra altura y, de hecho, podemos darnos el lujo de utilizar la altura dada junto al lado con que el que forma el ángulo de grados.
En nuestro ejercicio : El lado es o bien,
¿A qué conclusión llegamos?
La conclusión es que la fórmula para calcular el área de un triángulo rectángulo es el producto de los dos catetos dividido por Coloquemos en la fórmula y obtendremos:
El área del triángulo es
El cálculo del área de un triángulo obtuso es un poquito más complicado, pero te aseguro que desde el momento en que entiendas el principio básico, lograrás calcular el área del triángulo obtuso incluso durmiendo...
En ciertos casos, en un triángulo obtuso, se nos dará una altura que se encuentra fuera del triángulo.
Como por ejemplo en la siguiente ilustración:
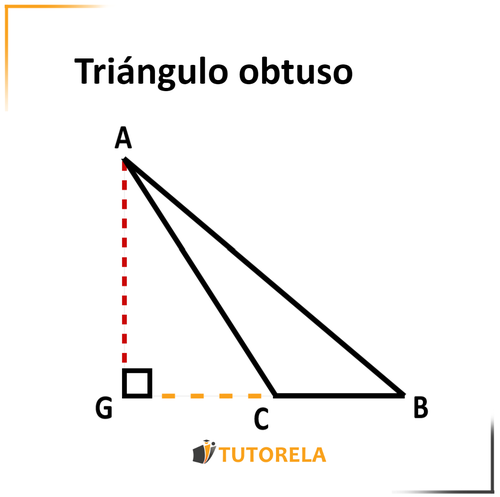
En esta ilustración se ha sacado la altura fuera del triángulo. En realidad, si continuáramos el lado (marcado en verde) formaría, junto a la altura, un ángulo recto.
¿cómo se calcula el área de un triángulo obtuso?
Recuerda las siguientes pautas y te irá bien:
Ahora resolvamos un ejercicio para que lo entiendas con más facilidad:
Dado el triángulo
Dado que:
Altura del triángulo
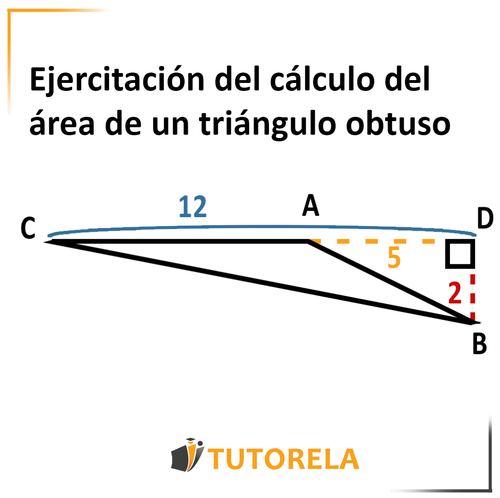
¿Cuál es el área del triángulo?
Solución:
Observemos que tenemos que la longitud del lado
y que el lado correspondiente que forma con él un ángulo de grados (la parte punteada fuera del triángulo) es
Si volvemos al primer punto que debíamos recordar - entenderemos que, para calcular el área debemos tomar en cuenta sólo la longitud de sin su continuación punteada.
Por lo tanto, lo veremos
Y ahora podremos colocar los datos con seguridad, de acuerdo con la fórmula básica:
El área del triángulo es
Si te interesa este artículo también te pueden interesar los siguientes artículos
En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Calcula el área del triángulo siguiente:
La fórmula de cálculo del área triangular es:
(el lado * la altura del lado que desciende al lado) /2
Es decir:
Ahora reemplazamos los datos existentes:
10
Calcula el área del triángulo ABC mediante los datos del dibujo:
En primer lugar, recordemos la fórmula para el área de un triángulo:
(el lado * la altura del desciende al lado) /2
En la pregunta tenemos tres datos, ¡pero uno de ellos es redundante!
Solo tenemos una altura, la línea que forma un ángulo de 90 grados - AD,
El lado al que desciende la altura es CB,
Por lo tanto, podemos usarlos en nuestro cálculo:
36 cm²
Calcula el área del triángulo rectángulo a continuación:
Como vemos que AB es perpendicular a BC y forma un ángulo de 90 grados
Se puede argumentar que AB es la altura del triángulo.
Entonces podemos calcular el área de la siguiente manera:
24 cm²
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
La fórmula para calcular el área de un triángulo es:
(lado * altura correspondiente al lado) / 2
Observa que en el triángulo que se nos proporciona, tenemos la longitud del lado pero no la altura.
Es decir, no tenemos datos suficientes para realizar el cálculo.
No se puede calcular
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
El triángulo que estamos viendo es el triángulo grande - ABC
El triángulo está formado por tres lados AB, BC y CA.
Ahora recordemos lo que necesitamos para el cálculo de un área triangular:
(lado x la altura que desciende del lado)/2
Por lo tanto, lo primero que debemos encontrar es una altura y un lado adecuados.
Se nos da el AC lateral, pero no hay altura que desciende, por lo que no nos sirve.
El lado AB no está dado,
Y así nos quedamos con el lado BC, que está dado.
Por el lado BC desciende la altura AD (los dos forman un ángulo de 90 grados).
Se puede argumentar que BC es también una altura, pero si profundizamos parece que CD puede ser una altura en el triángulo ADC,
y BD es una altura en el triángulo ADB (ambos son los lados de un triángulo rectángulo, por lo tanto son la altura y el lado).
Como no sabemos si el triángulo es isósceles o no, tampoco es posible saber si CD=DB, o cuál es su razón, y esta teoría falla.
Recordemos nuevamente la fórmula del área triangular y reemplacemos los datos que tenemos en la fórmula:
(lado* la altura que desciende del lado)/2
Ahora reemplazamos los datos existentes en esta fórmula:
17.4
Halla el área del triángulo mediante los datos de la figura:
Calcula el área del triángulo siguiente:
Calcula el área del triángulo ABC mediante los datos del dibujo: