El área del deltoidese puede calcular multiplicando las longitudes de las diagonales y dividiendo este producto por .
Área del deltoide:
¿Cómo calculamos el área del deltoide?
Fórmula del área del deltoide
Para facilitar la comprensión del concepto del cálculo, puede utilizar el siguiente dibujo y la fórmula que lo acompaña:
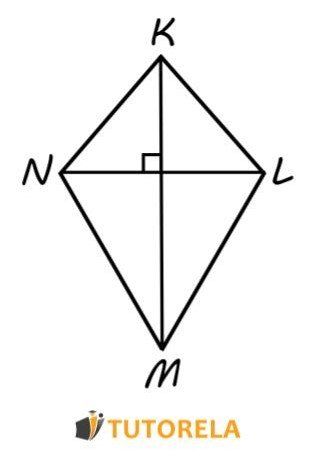
¡Pruébate en área del deltoide!
Indica la respuesta correcta
El cuadrilátero siguiente es:
Hay muchas formas geométricas que se pueden encontrar durante la resolución de problemas de ingeniería en todas las diferentes etapas de estudio, como en la escuela secundaria, en los exámenes de matriculación e incluso en psicometría. Una de las formas menos triviales es el deltoide y, como parte de las preguntas que lo rodean, a menudo se pide a los estudiantes que calculen el área del deltoide.
¿Qué es el deltoide?
Un deltoide es un polígono de cuatro lados (es decir, un cuadrilátero) con dos conjuntos distintos de lados adyacentes de igual longitud entre sí.
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Tipos de deltoides
Hay una clara distinción entre deltoide convexo y deltoide cóncavo.
Deltoide convexo
Deltoide convexo es un deltoide donde las diagonales están dentro y se cruzan entre sí. La diagonal más larga ejerce como una diagonal principal, mientras que la diagonal más corta ejerce como una diagonal secundaria.
Como puedes observar en el siguiente dibujo, la diagonal principal divide el deltoide en dos triángulos superpuestos, es decir, idénticos, y la diagonal secundaria divide el deltoide en dos triángulos isósceles cuyas bases son adyacentes y, de hecho, idénticas.
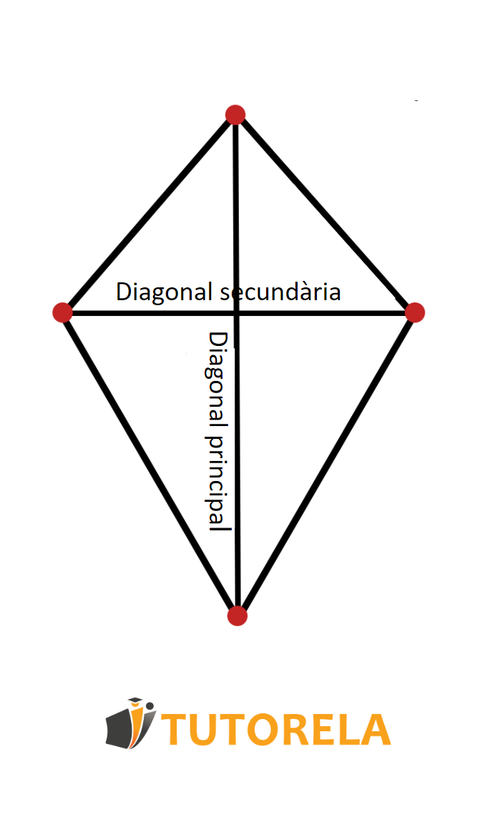
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Deltoide cóncavo
Deltoide cóncavo es un deltoide donde una de las diagonales (diagonal principal) pasa por dentro del deltoide y la otra diagonal (diagonal secundaria) pasa por fuera del deltoide.
El deltoide cóncavo se puede describir como una forma que consta de dos triángulos isósceles que comparten una base común, donde un triángulo contiene al otro triángulo. El siguiente dibujo describe mejor el deltoide cóncavo:
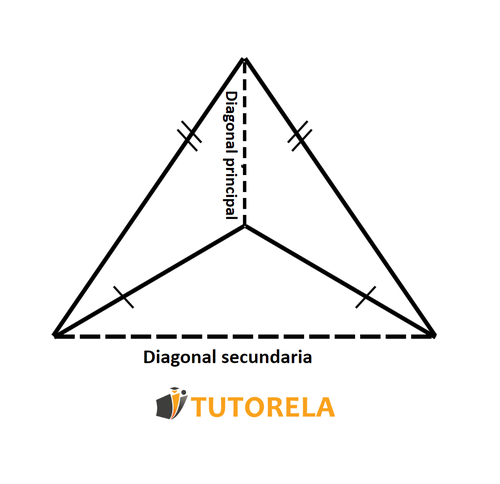
- Cuando todos los lados del deltoide tienen la misma longitud, se obtiene un rombo, que en realidad es un caso especial de deltoide.
- Otro caso especial de deltoide es un cuadrado, cuando se trata de un caso en el que todos los lados y todos los ángulos tienen el mismo tamaño.
Propiedades del deltoide
- Los ángulos laterales, o más precisamente, los ángulos entre los diferentes lados adyacentes del deltoide, son de igual tamaño.
- Las diagonales del deltoide son perpendiculares entre si
- La diagonal principal en el deltoide convexo (o su continuación en el deltoide cóncavo) cruza la diagonal secundaria (en ambos casos), y por lo tanto en realidad funciona como una perpendicular media
- La diagonal principal divide igualmente (cruza) los ángulos principales del deltoide
- Todo deltoide convexo tiene la posibilidad de bloquear un círculo
- En todo deltoide hay dos conjuntos de lados adyacentes de igual tamaño
- Como se mencionó, un deltoide cóncavo se caracteriza por una diagonal secundaria ubicada fuera del mismo
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Práctica del área de un deltoide
Ejercicio 1
Dado el deltoide cuya área es de cm², el punto de encuentro de las diagonales y .
Se debe calcular el área de la sección KP de acuerdo con el dibujo adjunto y los datos existentes:
- cm
- cm²
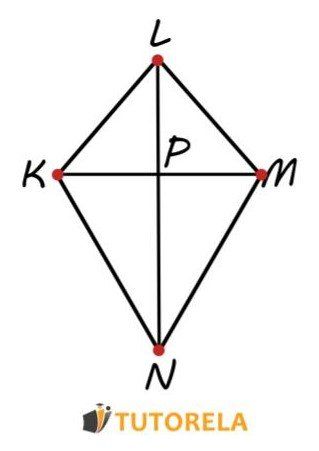
Solución:
Este ejercicio es un cálculo inverso, es decir, conocemos el área y se nos pide que calculemos la longitud del segmento .
En el primer paso, reemplazamos los datos que conocemos en la fórmula de área del deltoide.
Obtenemos:
Simplificamos la expresión y obtenemos:
De hecho, encontramos la longitud de la segunda diagonal del deltoide.
Según una de las propiedades del deltoide, la diagonal divide a la diagonal en dos partes iguales.
De aquí obtenemos que es igual a cm.
Respuesta:
cm
Ejemplos y ejercicios con soluciones de Área del deltoide o cometa
Ejercicio #1
Dado el deltoide ABCD
La diagonal AC=8 es el área del deltoide es 32 cm²
Calcula la diagonal DB
Solución en video
Solución Paso a Paso
Primero, recordamos la fórmula del área del deltoide: multiplicar las longitudes de las diagonales entre sí y dividir este producto por 2.
Reemplazamos los datos sabidos en la fórmula:
Simplificamos el 8 y el 2:
Dividimos por 4
Respuesta
8 cm
Ejercicio #2
Dado el deltoide de la figura:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
En un principio, recordemos la fórmula del área de un deltoide
Ambos datos ya existen, por lo que podemos colocarlos en la fórmula:
(4*7)/2
28/2
14
Respuesta
14
Ejercicio #3
Dado ABCD deltoide AB=BC DC=AD
Las diagonales del deltoide se cortan en el punto 0
Dado BD=14 El área del deloide es 42 cm²
Calcula el lado AO
Solución en video
Solución Paso a Paso
Reemplazamos los datos que tenemos en la fórmula del área del deltoide:
Diagonal por diagonal dividida por 2, reemplazamos los datos existentes en la fórmula:
Multiplicamos por 2 para deshacernos del denominador:
Dividimos por 14:
Prestemos atención que nos preguntaron sobre AO.
Se sabe que en un rombo, la diagonal principal cruza a la segunda diagonal, por lo tanto:
Respuesta
3 cm
Ejercicio #4
Indica la respuesta correcta
El cuadrilátero siguiente es:
Solución en video
Respuesta
Deltoide convexo
Ejercicio #5
Indica la respuesta correcta
El cuadrilátero siguiente es:
Solución en video
Respuesta
No es deltoide
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
- Altura del triángulo
- Deltoide
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Trapecios
- Área de un trapecio
- Perímetro de un trapecio
- Rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Área
- ¿Rombo, cometa o diamante?
- El área de un rombo
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









