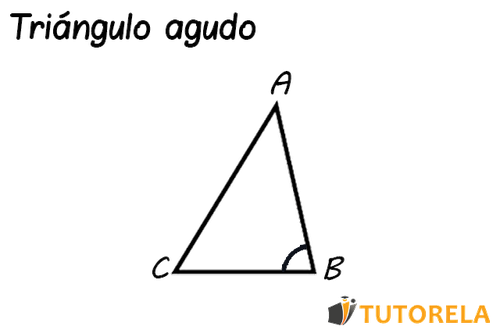
Un triángulo agudo tiene todos sus ángulos agudos, es decir, cada uno de sus tres ángulos mide menos de grados y la suma de los tres juntos resulta en grados.

Un triángulo agudo tiene todos sus ángulos agudos, es decir, cada uno de sus tres ángulos mide menos de grados y la suma de los tres juntos resulta en grados.

En un triángulo rectángulo, ¿el lado opuesto al ángulo recto se llama?
A continuación, veremos algunos ejemplos de triángulos agudos:
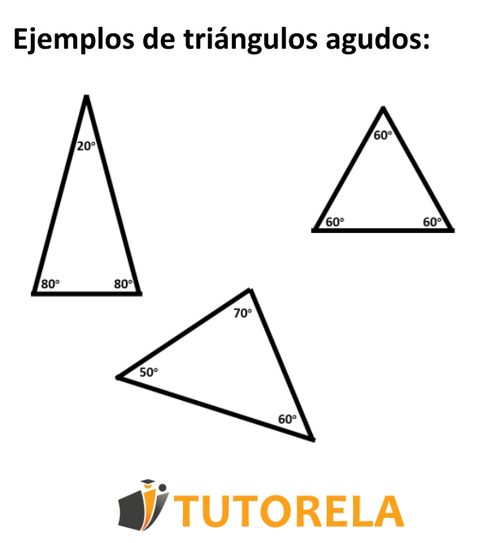
En estos ejemplos podemos observar triángulos con sus tres ángulos agudos, es decir, todos sus ángulos miden menos de .
Si está interesado en aprender más sobre otros temas de triángulos, puede ingresar a uno de los siguientes artículos:
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
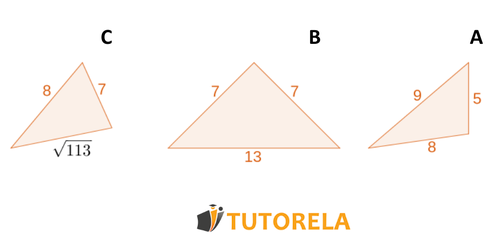
Tarea:
Determina cuál de los siguientes triángulos es obtuso, cuál es agudo y cuál es rectángulo:
Solución:
A. Examinaremos si el teorema de Pitágoras se cumple para este triángulo:
La suma de los cuadrados perpendiculares es mayor que el cuadrado sobrante, un triángulo con ángulos agudos.
B. Ahora examinaremos este triángulo:
La suma de los cuadrados perpendiculares es un pequeño supercuadrado, en un triángulo obtusángulo.
C. El lado más grande de los 3 se tratará como el resto.
El teorema de Pitágoras existe y por lo tanto el triángulo 3 es un rectángulo.
Respuesta:
A-ángulo agudo B-ángulo obtuso C-ángulo recto.
En un triángulo rectángulo, ¿cada uno de los dos lados que forman el ángulo recto se llama?
En un triángulo isósceles, ¿cada uno de los dos lados iguales se llama ?
En un triángulo isósceles, el ángulo entre dos ? se llama "ángulo ?"
Observemos 3 ángulos
Ángulo A es igual a
Ángulo B es igual a
Ángulo C es igual a
Tarea:
¿Estos ángulos pueden formar un triángulo?
Solución:
La suma de los ángulos en el triángulo son iguales a ,
por lo tanto estos ángulos pueden formar un triángulo.
Respuesta:
Si, ya que la suma de los ángulos internos de un triángulo es igual a .
Ángulo A es igual a
Ángulo B es igual a
Ángulo C es igual a
Tarea:
¿Estos ángulos pueden formar un triángulo?
Solución:
La suma de los ángulos es mayor a ,
por lo tanto estos ángulos no pueden formar un triángulo.
Respuesta:
No, ya que la suma de los ángulos internos debe ser , y en este caso los ángulos son iguales a .
¿El triángulo del dibujo es un triángulo rectángulo?
¿El dibujo muestra un triángulo obtuso?
¿El dibujo muestra un triángulo obtuso?
¿Cuáles son los 6 tipos de triángulos?
Como bien sabemos un triángulo es una figura geométrica el cual tiene tres lados, existen diferentes tipos de triángulos de acuerdo a su medida y a sus ángulos. Los cuales se mencionaran a continuación:
- Triángulo acutángulo
- Triángulo recto
- Triángulo obtusángulo
¿Qué es un triángulo agudo?
Un triángulo agudo es aquel en donde todos los ángulos son menores a , es decir, todos sus ángulos son ángulos agudos.
Ejemplos de triángulos agudos
Ya se mencionó que un triángulo agudo es un triángulo con tres ángulos agudos, por lo tanto se mostraran a continuación algunos triángulos con medidas de ángulos menores a en todas sus esquinas.

Triangulo con medidas 60°, 40° y 80°

Triángulo con medidas de 50°, 70° y 60°

Triángulo con medidas de 65°, 50°, 65°
¿El triángulo del dibujo es un triángulo rectángulo?
Se puede observar que todos los ángulos en el triángulo dado son menores de 90 grados.
En un triángulo rectángulo debe haber un ángulo igual a 90 grados.
Como este dato no existe, el triángulo no es un triángulo rectángulo.
No
En un triángulo rectángulo, ¿la suma de los dos ángulos no rectos es ?
En un triángulo rectángulo hay un ángulo igual a 90 grados, los otros dos ángulos suman 90 grados (180° es la suma de los ángulos en un triángulo)
Por lo tanto, la suma de los dos ángulos no rectos es 90 grados.
90 grados
Elija el triángulo apropiado según la figura:
Ángulo B es igual a 90 grados
Tengamos en cuenta que los triángulos en el ángulo B forma un ángulo recto, es decir, un ángulo de 90 grados.
En las respuestas c+d puedes ver que el ángulo B es menor a 90 grados.
La respuesta a es igual a 90 grados.
Cuál triángulo es el siguiente
Dado que en un triángulo obtusángulo basta con que uno de los ángulos sea mayor que 90°, y en el triángulo dado tenemos un ángulo C mayor que 90°,
Además, la suma de los ángulos del triángulo dado es 180 grados:
El triángulo es obtusángulo.
Triángulo obtusángulo
¿Qué triángulo se da en el dibujo?
La medida del ángulo C es de 90°, por lo tanto es un ángulo recto.
Si uno de los ángulos del triángulo es recto, es un triángulo rectángulo.
Triángulo rectángulo
Dados los valores de los lados de un triángulo, ¿es un triángulo con lados diferentes?
Dados los valores de los lados de un triángulo, ¿es un triángulo con lados diferentes?
¿El triángulo del dibujo es un triángulo acutángulo?