Función, describe una correlación o coincidencia entre una variable dependiente () y una variable independiente (). La legitimidad de esta relación entre las variables se denomina "regla de correspondencia".
Representación verbal y tabular de una función
Representación verbal de una función
La representación verbal de una función expresa la legitimidad entre las variables verbalmente, es decir, a través de una historia.
Una formulación clásica para una representación verbal de una función puede verse así:
- Suponiendo que Daniel lee todos los libros que compra ese mes, la cantidad total de libros que Daniel lee por año () es una función de la cantidad de libros que Danny compra cada mes ().
Representación tabular de una función
Una representación tabular de una función es una demostración de la legitimidad de una función utilizando una tabla de valores (variable independiente) y de los valores correspondientes (variable dependiente).
Por lo general, una tabla de valores se muestra de la siguiente manera:
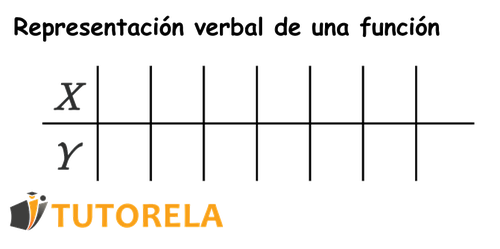
¡Pruébate en formas de representar una función!
¿La gráfica dada es una función?
Ejemplos de ejercicios sobre representación verbal y tabular de una función
Ejemplo 1
es una función de que corresponde a cualquier valor de , un número menor que él en .
Resuelva la ecuación para cada uno de los números de representados en la siguiente tabla y coloque el número correcto en .
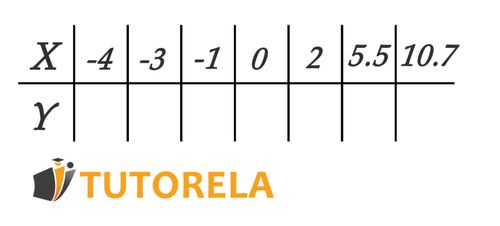
Si , entonces Y será igual a ____________
Si , entonces Y será igual a ___________
Un valor de correspondiente a es __________
Un valor correspondiente a es __________
Determine si los datos de la siguiente tabla representan una función constante
Determina si la siguiente tabla representa una función
¿La gráfica dada es una función?
Práctica de representación verbal y tabular de una función
Ejemplo 2
Describe en palabras la relación entre e .
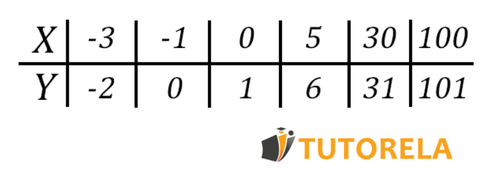
Ejemplo 3
Anote qué tabla representa una función y cuál no representa una función

¿La gráfica dada es una función?
¿La gráfica dada es una función?
¿La gráfica dada es una función?
Ejemplo 4
es una función de que corresponde a cualquier valor de , un número que es veces mayor que él.
Completa la tabla de valores
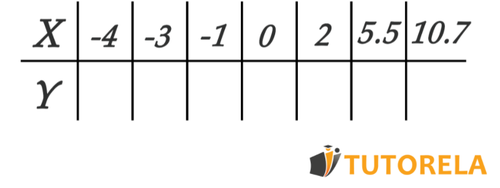
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
Ejemplo 5
es una función de que corresponde a cualquier valor de un número veces menor que él.
Completa la tabla de valores

- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
Determina si la siguiente tabla representa una función
Determina si la siguiente tabla representa una función
Determina si la siguiente tabla representa una función
Ejemplo 6
Completa la siguiente tabla
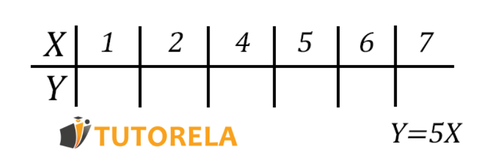
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
Ejemplo 7
Responda las siguientes preguntas (en cada uno de los ejemplos, escriba una tabla de valores y dibuje la gráfica)
- Escribe un ejemplo de una función cuya gráfica la describe como una gráfica continua
- Escribe un ejemplo de una función, cuya gráfica sea discreta
¿La gráfica dada es una función?
¿La gráfica dada es una función?
Determina si la siguiente tabla representa una función
Ejemplo 8
La función corresponde a cualquier número que sea su raíz.
Completa la tabla de valores

- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
Ejemplo 9
La función corresponde a cualquier número menor en de la mitad del número
- Completa la tabla de valores

- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
¿Cuál de las siguientes ecuaciones corresponde a la función representada en la gráfica?
¿Cuál de las siguientes ecuaciones corresponde a la función representada en la gráfica?
¿La gráfica dada es una función?
Ejemplo 10
La función corresponde a cualquier número mayor en veces del número
- Completa la tabla de valores

- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
- Si , entonces será igual a ____________
Preguntas de repaso
¿Qué es una función?
Una función es una relación que hay entre dos variables, la variable la cual lleva el nombre de variable dependiente, y la variable , a la cual se le llama variable independiente, entre estas dos variables existe una regla de correspondencia; es decir, para cada valor de le corresponde un único valor de .
¿Cuáles son las formas de representar una relación?
Una función se puede representar de la siguiente manera:
- Verbalmente
- Algebraicamente
- Tabla de valores (Tabular)
- Gráficamente.
¿Cómo representar funciones paso a paso?
Veamos un ejemplo de la manera en cómo se debe de representar una función
Ejemplo:
Representar la siguiente función es sus diferentes formas
- Verbalmente:
Sea una función de de tal manera que corresponda un valor de un número aumentado en
- Algebraicamente:
- Tabla de valores:
Ya tenemos la función en forma algebraica, ahora vamos a darle valores a , para encontrar el valor de , de acuerdo a la regla de correspondencia, y estos valores los vamos registrando en una tabla:
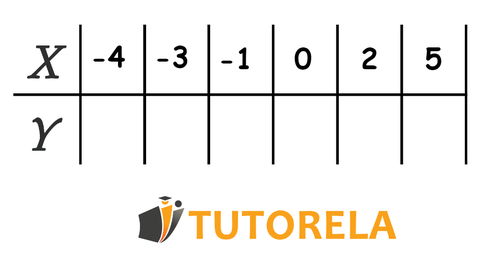
Ahora bien vamos a ir sustituyendo los valores de , para ir registrando el valor que le corresponde a , empecemos
Ya sabemos que la expresión algebraica de esta función es:
Entonces,
Cuando
Cuando
Cuando
Cuando
Cuando
Cuando
De acuerdo a estos datos ahora vamos a registrarlo en la tabla
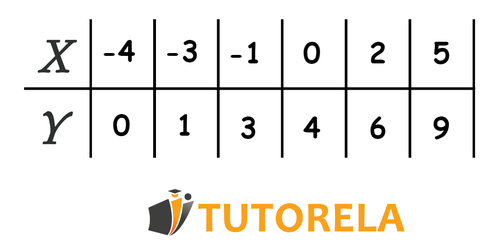
Hemos representado la función en una tabla de valores.
- Gráficamente:
Por último vamos a representar estos valores en una gráfica:
Vamos a buscar los pares de coordenadas en el plano cartesiano, y unimos cada punto de la siguiente manera
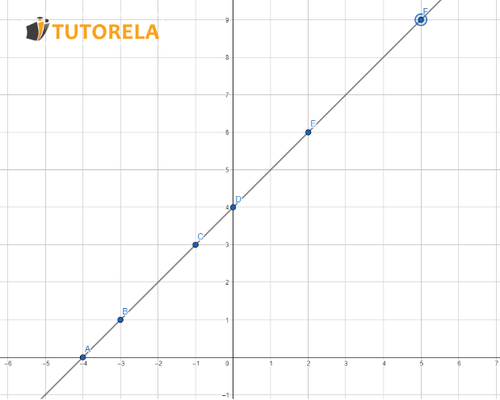
Podemos observar que la función en forma gráfica es una función lineal por formarse una línea recta.
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Representación gráfica de una función
Representación algebraica de una función
Asignación de valor numérico en una función
Intervalos de crecimiento y de decrecimiento de una función
En la página web de Tutorela encontrarás una variedad de artículos con interesantes explicaciones sobre matemáticas
Determine si los datos de la siguiente tabla representan una función constante
Determina si la siguiente tabla representa una función
¿La gráfica dada es una función?
ejemplos con soluciones para Representación verbal y tabular de una función
Ejercicio #1
¿La gráfica dada es una función?
Solución en video
Respuesta
No
Ejercicio #2
Determine si los datos de la siguiente tabla representan una función constante
Solución en video
Respuesta
No
Ejercicio #3
Determina si la siguiente tabla representa una función
Solución en video
Respuesta
No
Ejercicio #4
¿La gráfica dada es una función?
Solución en video
Respuesta
No
Ejercicio #5
¿La gráfica dada es una función?
Solución en video
Respuesta
No
- Valor absoluto y desigualdad con valor absoluto
- Sistema de coordenadas
- Par ordenado
- Gráfico
- Lectura de información de gráficos
- Tabla de valores
- Gráfica discreta
- Gráfica continua
- Funciones para séptimo grado
- Intervalos de crecimiento y de decrecimiento de una función
- Función creciente
- Función decreciente
- Función constante
- Intervalo de decrecimiento de la función
- Intervalos de función creciente
- Dominio de una función
- Función indefinida
- Asignación de valor numérico en una función
- Tasa de variación de una función
- Variación de una función
- Tasa de variación representada con peldaños en la gráfica de la función
- Tasa de variación de una función representada gráficamente
- Tasa de variación constante
- Tasa de variación inconstante
- Tasa de variación de una función representada por una tabla de valores
- Método algebraico
- Factorización: Extracción de factor común
- La propiedad distributiva: ampliación
- Desigualdades
- Inequations (con valor absoluto)
- Función lineal
- Representación gráfica de una función que representa una proporcionalidad directa
- La función lineal y=mx+b
- Hallar ecuación lineal
- Positividad y negatividad de una función lineal
- Representación de fenómenos usando funciones lineales
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









