Si está interesado en aprender más sobre otros temas de ángulos, puede ingresar a uno de los siguientes artículos:
En la página web de Tutorela encontrarás una gran variedad de artículos sobre matemáticas
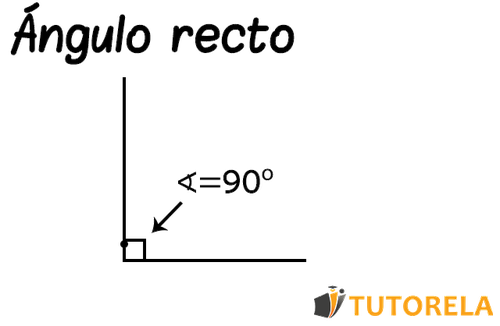
Varios ejemplos de Ángulos rectos
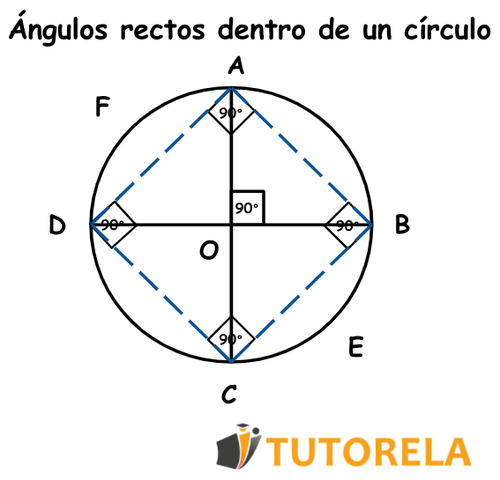
Ángulos rectos dentro de un círculo
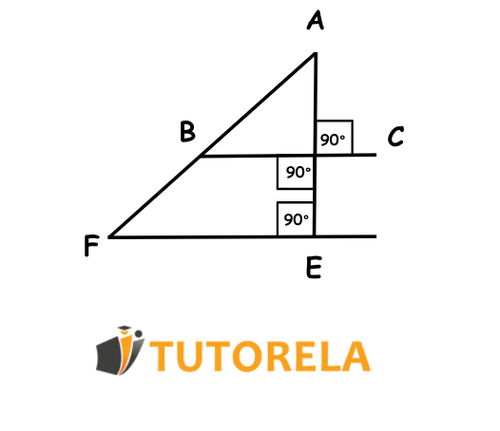
Ángulos rectos dentro en un triángulo
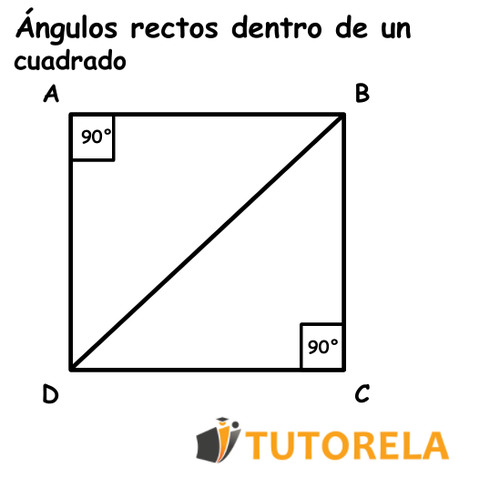
Ángulos rectos dentro de un cuadrado
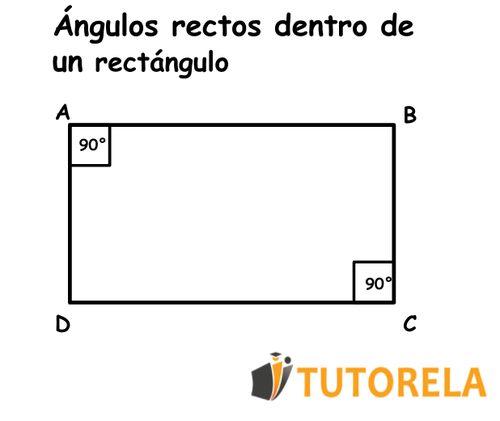
Ángulos rectos dentro de un rectángulo
¡Únete a 30,000 estudiantes destacados en matemáticas!
Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy
Comprueba tu conocimiento
Ejercicios
Ejercicio 1 (sobre rectas paralelas)
Esta pregunta se divide en varias partes:
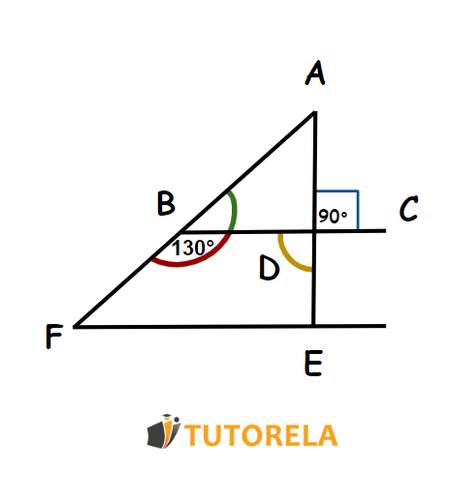
- ¿Cuántos grados es el ángulo de ∡ABC y qué tipo de ángulo es en relación con ∡CBF?
- ¿Cuántos grados es el ángulo ∡BDE y qué tipo de ángulo es en relación con el ∡ADC?
Respuesta 1:
A. El ángulo de ∡ABC es igual a 180º−130º=50º
B. El ángulo de ∡ABC con respecto al ángulo de ∡CBF se llama Ángulos adyacentes
Respuesta 2:
- El ángulo ∡BDE es igual a 90º ya que es un ángulo opuesto por el vértice con respecto al ángulo ∡ADC=90º
Ejercicio 2
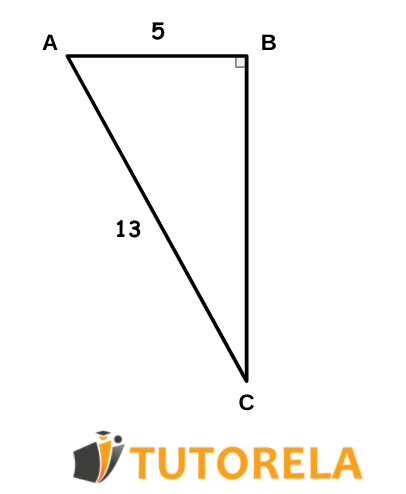
Dado el triángulo △ABC:
Tarea:
Encontrar la longitud de BC
Solución:
Teorema de Pitágoras - Aplicar la fórmula
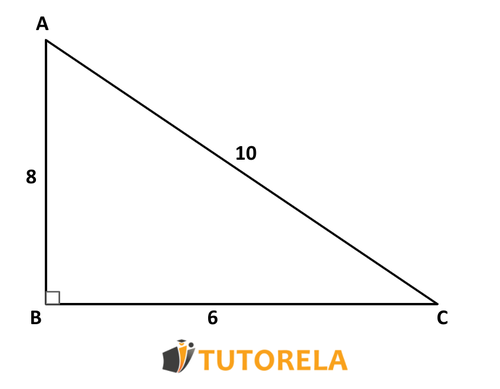
Dado el triángulo △ABC en el dibujo.
Consigna:
Encontrar la longitud de BC
Solución:
Escribir el Teorema de Pitágoras del triángulo rectángulo △ABC
AB2+BC2=AC2
Colocamos las longitudes conocidas:
52+BC2=132
25+BC2=169
BC2=169−25=144,
Ahora sacando la raíz tenemos que:
BC=12
Respuesta:
12 cm.
¿Sabes cuál es la respuesta?
Ejercicio 3
Tarea:
Frente a usted hay un triángulo rectángulo, calcular su área.
Solución:
Calcular el área del triángulo a partir de la fórmula de cálculo del área del triángulo rectángulo.
2cateto×cateto
2AB⋅BC=28⋅6=248=24
Respuesta:
La respuesta es 24 cm².
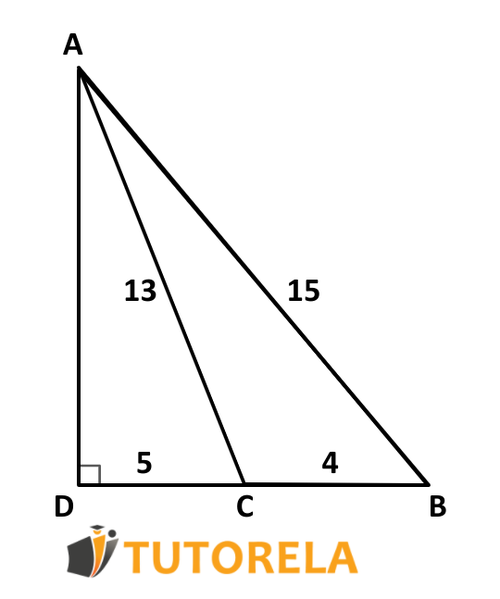
Ejercicio 4
Tarea:
Dado el triángulo rectángulo △ADB
El perímetro del triángulo △ADC es igual a 30 cm.
Dado:
AB=15
AC=13
DC=5
CB=4
Calcular el área del triángulo △ABC
Solución:
Dado el perímetro del triángulo △ADC igual a 30 cm.
Desde aquí podemos calcular a AD.
AD+DC+AD=PerıˊmetroΔADC
AD+5+13=30
AD+18=30
Restamos 18 de ambos lados de la igualdad
AD=12
Ahora podemos calcular el área del triángulo ΔABC
Prestar atención: hablamos de un triángulo obtusángulo por lo tanto su altura es AD.
Usamos la fórmula para calcular el área del triángulo:
2ladoaltura×lado=
2AD⋅BC=212⋅4=248=24
Respuesta:
El área del triángulo ΔABC es igual a 24 cm².
Comprueba que lo has entendido
Ejercicio 3 Incorrecto
Respuesta correcta: Todas las respuestas son incorrectas.
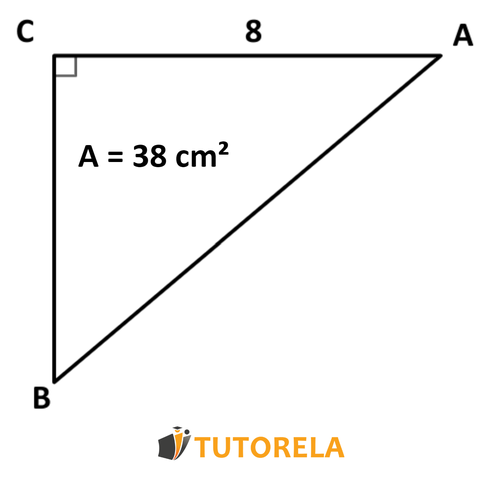
Ejercicio 5
Tarea:
Dado el triángulo ΔABC rectángulo
El área del triángulo es igual a 38 cm², AC=8
Encontrar la medida del cateto BC
Solución:
Calcularemos la longitud de BC desde la fórmula de cálculo del área del triángulo rectángulo:
2cateto×cateto
2AC⋅BC=28⋅BC=38
Multiplicamos la ecuación por el común denominador
/ ×2
Después dividimos la ecuación por el coeficiente de BC
8×BC=76
Dividimos entre 8
BC=9.5
Respuesta:
El largo del cateto BC es igual a 9.5 centímetros.
Ejercicio 6
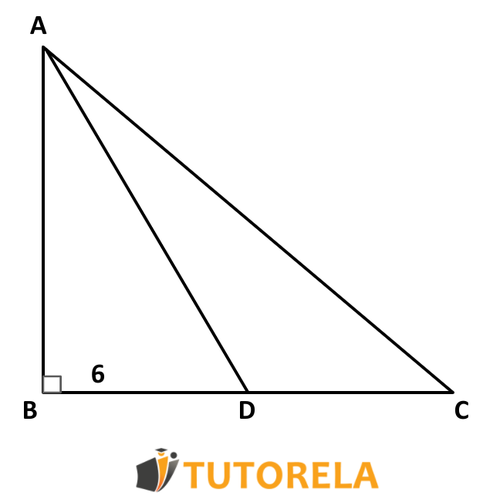
Frente a usted, hay un triángulo rectángulo ΔABC.
Dado que BC=6
El largo del cateto AB es mayor en 3331% que el largo de BD.
El área del triángulo ΔADC es mayor en un 25 que el área del triángulo ΔABD.
Tarea:
¿Cuál es el área del triángulo ΔABD?
Solución:
Para encontrar la medida del cateto AB utilizaremos el dato que su largo es mayor en 33.33 que el largo de BD.
AB=1.33333⋅BD
(100100+10033.33=100133.33=1.333)
AB=1.333⋅6=8
Ahora calcularemos el área del triángulo de ΔABD.
SΔABD=2AB⋅BD=28⋅6=248=24
Respuesta:
24 cm².
¿Crees que podrás resolverlo?
Ejercicio 7
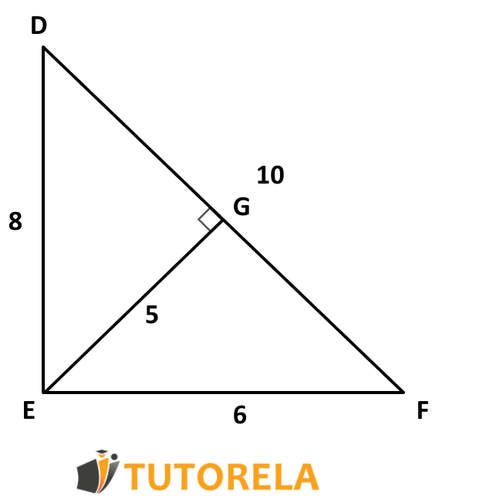
Tarea:
¿En qué datos de la gráfica hay un error?
Para que el área del triángulo sea de 24 cm², y cuál es el dato que debe estar en lugar del error?
Solución:
Explicación: área del triángulo rectángulo.
SΔEDF=2ED⋅EF=28⋅6=248=24
Según la fórmula:
2cateto×cateto
Si se puede calcular el área del triángulo también desde la fórmula de:
2lado×alturadellado
2EG×10=24
Multipliquemos ambos lados del igual ×2
10EG=48
Ahora dividamos :10
EG=4.8
Respuesta:
El dato erróneo es EG.
El largo de EG debe ser 4.8 cm.
Ejercicio 8
En el siguiente ejemplo, se presenta un cuadrado ABCD.
A. El ángulo ∡ABC es igual al ángulo de ∡ADC? ¿Se puede decir que BD sirve como bisectriz del ángulo ∡ABC?
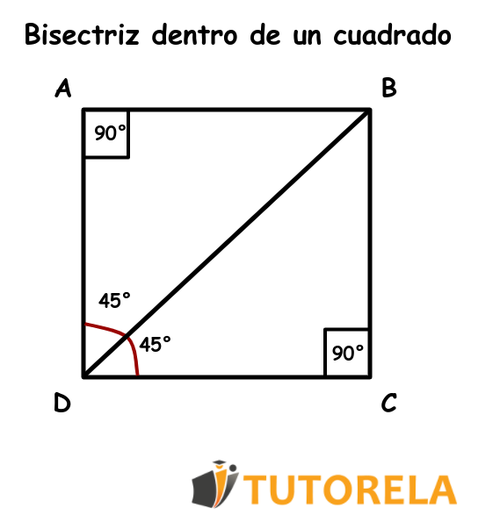
Solución al ejercicio 2:
La recta BD creó 2 puntos donde el ángulo se dividió en 2 ángulos iguales.
Respuesta:
Por lo tanto, DB es una bisectriz de los dos ángulos ∡ADC y ∡ABC
Comprueba tu conocimiento
ejemplos con soluciones para Ángulo recto
Ejercicio #1
Verdadero o falso
Uno de los ángulos del rectángulo puede ser un ángulo agudo.
Solución en video
Solución Paso a Paso
Una de las propiedades de un rectángulo es que todos sus ángulos son rectos.
Por lo tanto, no es posible que un ángulo sea agudo, es decir, menor de 90 grados.
Respuesta
Ejercicio #2
Elija el triángulo apropiado según la figura:
Ángulo B es igual a 90 grados
Solución en video
Solución Paso a Paso
Tengamos en cuenta que los triángulos en el ángulo B forma un ángulo recto, es decir, un ángulo de 90 grados.
En las respuestas c+d puedes ver que el ángulo B es menor a 90 grados.
La respuesta a es igual a 90 grados.
Respuesta
Ejercicio #3
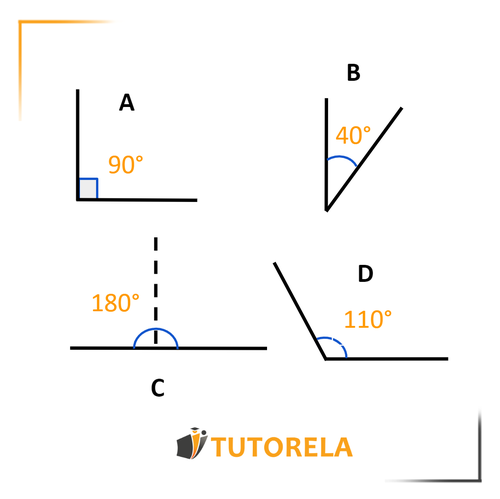
¿Cuál de los siguientes ángulos es un ángulo plano?
Solución en video
Respuesta
Ejercicio #4
¿En cuál de las figuras está marcado un ángulo recto?
Solución en video
Respuesta
Ejercicio #5
¿En cuál de las figuras está marcado un ángulo recto?
Solución en video
Respuesta