Cuando los estudiantes escuchan las palabras "figuras compuestas", generalmente se sienten incómodos. Justo antes de que también te preguntes: "Oh, ¿por qué esto otra vez?", debes saber que no hay una razón real. Describir las figuras como compuestas no las hace realmente así. Resulta que calcular áreas y perímetros de figuras compuestas es en realidad relativamente sencillo.
¿Cómo calculamos el área de figuras complejas?
¿Cómo calculamos el área de figuras complejas?
Serás introducido a las figuras complejas solo después de que aprendas varias figuras en geometría. La razón por la que estas figuras son complejas se debe al hecho de que son ligeramente diferentes de las que has llegado a conocer. En cada figura compleja, hay figuras adicionales ocultas que necesitas identificar. Dividir la figura compleja en varias figuras diferentes (y familiares) te permitirá responder a la pregunta de cómo calcular el área de figuras complejas.
El truco: extraer una forma familiar dentro de la forma compleja
Entonces, ¿cómo respondemos a la pregunta de cómo calcular el área de figuras complejas? Primero, necesitas identificar figuras familiares dentro de la figura compleja. Un ejemplo de esto: un rectángulo. Como sabes, cada figura tiene propiedades que conoces, así que dentro de la figura compleja, puedes aplicar las propiedades de la figura familiar y así calcular áreas y perímetros.
Después de completar los datos faltantes (según las propiedades de cada figura, por ejemplo: rectángulo), puedes completar el "rompecabezas", identificar datos adicionales que se te revelan y así calcular el área de la figura compleja. Al calcular el área de figuras complejas, a menudo necesitarás realizar operaciones aritméticas simples como división y suma (principalmente para los lados de la figura) - todo basado en las propiedades únicas de cada figura.
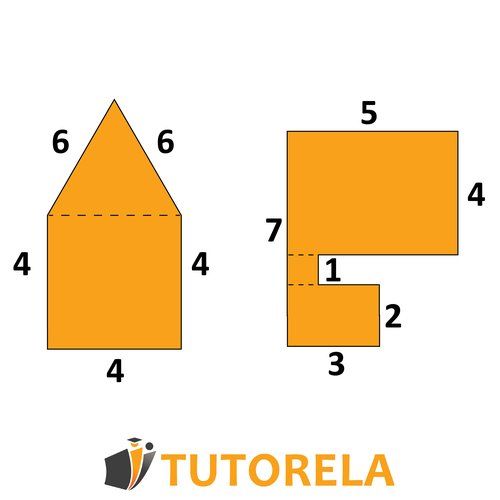
¡Pruébate en área del rectángulo!
Calcula el área del paralelogramo según los datos.
¿Cómo calculamos el área de figuras complejas?
Cuando los estudiantes escuchan las palabras "figuras compuestas", generalmente se sienten incómodos. Justo antes de que también te preguntes: "Oh, ¿por qué esto otra vez?", debes saber que realmente no hay razón. Describir las figuras como compuestas no las hace realmente así. Resulta que calcular áreas y perímetros de figuras compuestas puede ser relativamente sencillo.
Serás introducido a las figuras complejas solo después de que aprendas varias figuras en geometría. La razón por la que estas figuras son complejas se debe al hecho de que son ligeramente diferentes de las que has llegado a conocer. En cada figura compleja, hay figuras adicionales ocultas que necesitas identificar. Dividir la figura compleja en varias figuras diferentes (y familiares) te permitirá responder a la pregunta de cómo calcular el área de figuras complejas.
El truco: extraer una forma familiar dentro de la forma compleja
Entonces, ¿cómo respondemos a la pregunta de cómo calcular el área de figuras complejas? Primero, necesitas identificar figuras familiares dentro de la figura compleja. Por ejemplo: un rectángulo. Como sabes, cada figura tiene propiedades que conoces, así que dentro de la figura compleja, puedes aplicar las propiedades de la figura familiar y así calcular áreas y perímetros.
Después de completar los datos faltantes (según las propiedades de cada figura, por ejemplo: rectángulo), puedes completar el "rompecabezas", identificar datos adicionales que se hacen evidentes y así calcular el área de la figura compuesta. Al calcular el área de figuras compuestas, frecuentemente necesitarás realizar operaciones aritméticas simples como división y suma (especialmente para los lados de la figura) - todo basado en las propiedades únicas de cada figura.
Por ejemplo: Suponiendo que la figura compuesta incluye varios rectángulos diferentes, según las longitudes de los lados dadas, será posible calcular las diferentes áreas. El área de un rectángulo se calcula usando la fórmula largo X ancho. Cuando las longitudes de los lados son visibles, se pueden realizar restas y sumas (según los tamaños de los rectángulos y sus posiciones dentro de la figura) de los lados, y así calcular el área de la figura, como se ve en el ejemplo a continuación.
Para calcular el área de la figura - la dividiremos de manera que cree dos rectángulos. Encontraremos el área sumando y/o restando rectángulos.
En esta división creamos:
Un rectángulo con tamaño rectángulo
Un rectángulo con tamaño rectángulo
El área de la forma compuesta completa es:
o
Completa la oración
Para encontrar el área de un triángulo rectángulo, se debe multiplicar a _ entre sí y dividir por 2.
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
ejemplos con soluciones para Área del rectángulo
Ejercicio #1
Calcula el área del paralelogramo según los datos.
Solución en video
Solución Paso a Paso
Como sabemos que ABCD es un paralelogramo, según las propiedades del mismo todo par de lados opuestos son iguales y paralelos.
Por lo tanto
Calculamos el área del paralelogramo según la fórmula de lado por la altura que desciende de ese lado, por lo tanto el área del paralelogramo es igual a:
Respuesta
70
Ejercicio #2
Calcula el área del triángulo siguiente:
Solución en video
Solución Paso a Paso
La fórmula de cálculo del área triangular es:
(el lado * la altura del lado que desciende al lado) /2
Es decir:
Ahora reemplazamos los datos existentes:
Respuesta
10
Ejercicio #3
Dado el siguiente rectángulo:
Halla el área del rectángulo.
Solución en video
Solución Paso a Paso
Calculemos el área del rectángulo multiplicando el largo por el ancho:
Respuesta
10
Ejercicio #4
Dado el trapecio:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Fórmula del área de un trapecio:
Reemplazamos los datos en la fórmula y resolvemos:
Respuesta
52.5
Ejercicio #5
El ancho del rectángulo es igual a 15 cm y el largo es igual a 3 cm
Calcula el área del rectángulo
Solución en video
Solución Paso a Paso
Para calcular el área del rectángulo, multiplicamos el largo por el ancho:
Respuesta
45
Más preguntas
Area of a Triangle
- Cálculo del Área de un Triángulo: Base 5 y Altura 6
- Cálculo del Área de un Triángulo Rectángulo: Lados 5, 7 y 8.6 Unidades
- Cálculo del Área del Triángulo ABC: AC=10cm, AD=3cm, BC=11.6cm
- Calcula la Altura X en un Triángulo Rectángulo con Área 20 y Base 5
- Área de Triángulo con Altura 7 y Base 8.5: ¿Es Posible Calcularlo?
- Líneas paralelas (Rectas paralelas)
- Ángulos en rectas paralelas
- Ángulos alternos
- Ángulos correspondientes
- Ángulos colaterales
- Ángulos opuestos por el vértice
- Ángulos adyacentes
- El Teorema de Pitágoras
- Altura del triángulo
- Elementos de la circunferencia
- Círculo
- Diámetro
- Pi
- Área de un circulo
- Perímetro de un circulo
- El centro de la circunferencia
- Radio
- ¿Cómo se calcula el radio mediante su circunferencia?
- Triángulos congruentes
- Deltoide
- Área del deltoide:
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Maneras de identificar paralelogramos
- Simetría rotacional en paralelogramos
- Del cuadrilátero al paralelogramo
- Semejanza de triángulos y polígonos
- Criterios de semejanza de triángulos
- Trapecios
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- Área de un trapecio
- Perímetro de un trapecio
- Trapecio isósceles
- Rectángulo
- De un cuadrilátero a un rectángulo
- Del paralelogramo al rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Cuadrado
- El área de un cuadrado
- De paralelogramo a cuadrado
- Segmento medio
- Segmento medio de un triángulo
- Segmento medio de un trapecio
- Área
- ¿Rombo, cometa o diamante?
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
- El área de un rombo
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Prisma rectangular (ortoedro)
- El cubo
- Cómo calcular el área de superficie de un prisma rectangular (ortoedro)
- Cómo calcular el volumen de un prisma rectangular (ortoedro)
- Área lateral de un ortoedro
- Prisma triangular recto
- Las bases del prisma triangular recto
- Las caras laterales del prisma
- Aristas laterales de un prisma
- Altura del prisma
- El volumen del prisma
- Área de superficie de prismas triangulares
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Ángulos exteriores correspondientes
- Ángulos alternos internos
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- Partes de un Círculo
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









