En este artículo aprenderemos qué es el área y, entenderemos cómo se calcula para cada figura, del modo más práctico y sencillo que hay.
¿Empezamos?
Área
¿Qué es el área?
Área es la definición del tamaño de algo. En las matemáticas, justamente lo que nos interesa ahora, se trata del tamaño de alguna figura.
En la vida diaria seguramente habrás oído hablar de área en relación con la superficie de un departamento, parcela de terreno, etc.
De hecho, cuando preguntan cuál es la superficie de tu departamento, están preguntando sobre su tamaño y, en lugar de responder con palabras como «grande» o «pequeño» podemos calcular su área y expresarla con unidades de medida. De este modo podemos comparar distintos tamaños.
Unidades de medida de la superficie
Superficies grandes como departamentos suelen medirse en metros, por consiguiente, la unidad de medida será metro cuadrado.
En cambio, figuras más pequeñas se miden, por lo general, en centímetros, es decir, la unidad de medida de la superficie será centímetro cuadrado.
Recuerda:
Unidades de medida de la superficie en
Unidades de medida de la superficie
¡Pruébate en área del cuadrado!
Calcula el área del paralelogramo según los datos.
Área
¡Ahora aprenderemos a calcular la superficie de (casi) todas las figuras que conocemos! ¿Estamos listos?
Área del cuadrado
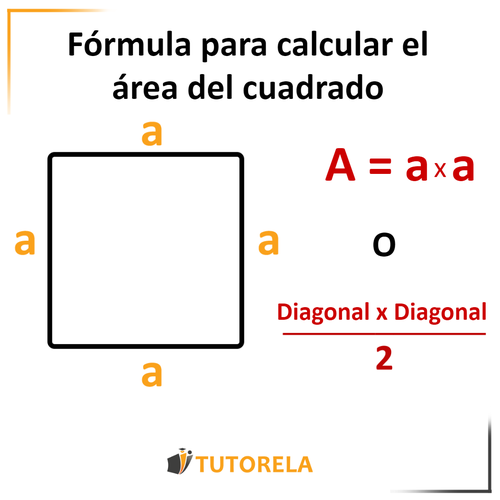
Lado del cuadrado
Multiplicaremos el lado del cuadrado por sí mismo
Otro modo:
Para obtener más información, ingresa al link de Área del cuadrado
Completa la oración
Para encontrar el área de un triángulo rectángulo, se debe multiplicar a _ entre sí y dividir por 2.
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Área del rectángulo
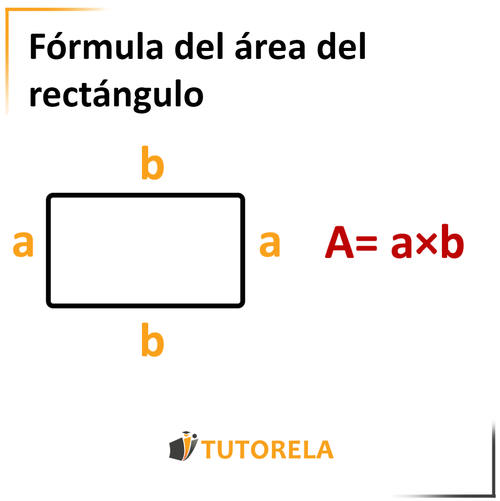
Multiplicaremos un lado del rectángulo por el lado contiguo (el lado con el que forma un ángulo de grados)
Para obtener más información, ingresa al link de Área del rectángulo
Área del triángulo
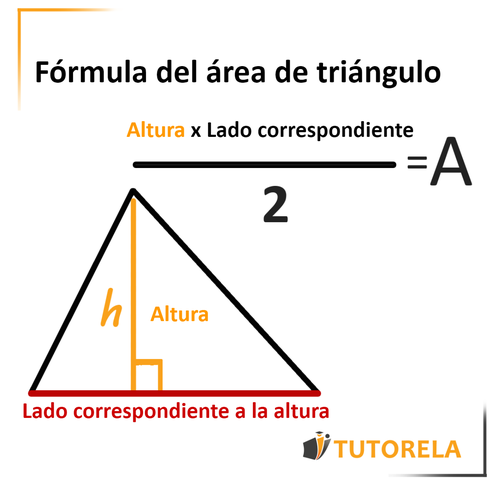
Multiplicaremos la altura por el lado correspondiente - o sea, el lado con el cual forma un ángulo de grados y dividiremos el producto por .
Para obtener más información, ingresa al link de Área del triángulo
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Área del rombo
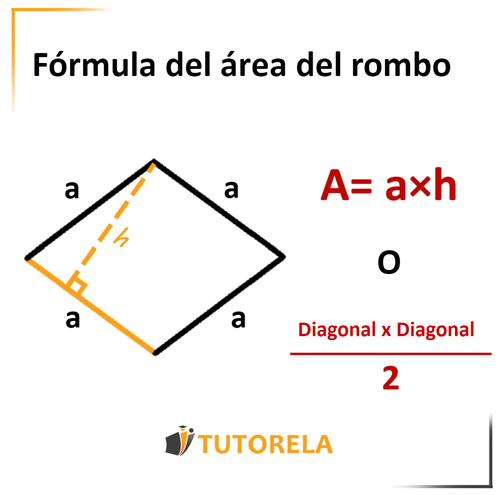
–> Lado del rombo
–> Altura
Multiplicaremos la altura por el lado correspondiente o sea, el lado con el cual forma un ángulo de grados.
Otro modo :
Para obtener más información, ingresa al link de Área del rombo
Área del paralelogramo
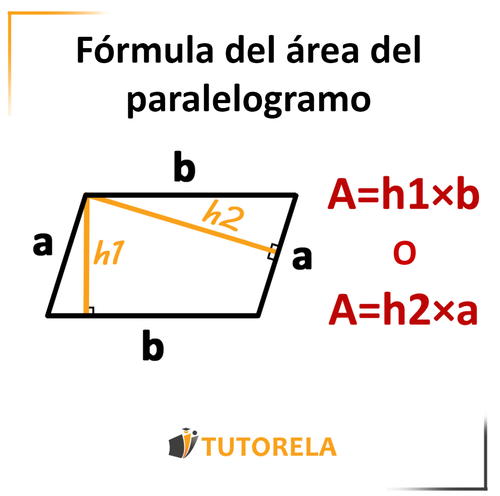
–> Altura
–> El lado que forma un ángulo de grados con la altura .
Multiplicaremos la altura por el lado al cual llega la altura y forma con él un ángulo de grados .
Para obtener más información, ingresa al link de Área del paralelogramo
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Área del círculo
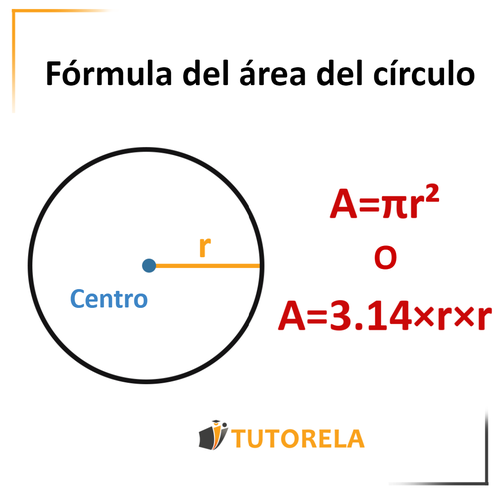
El radio de la circunferencia
PI
Se calculará como el número
Multiplicaremos PI por dos veces el radio de la circunferencia, o sea
O, más sencillo, la fórmula es:
Para obtener más información, ingresa al link de Área del círculo
Área del trapecio
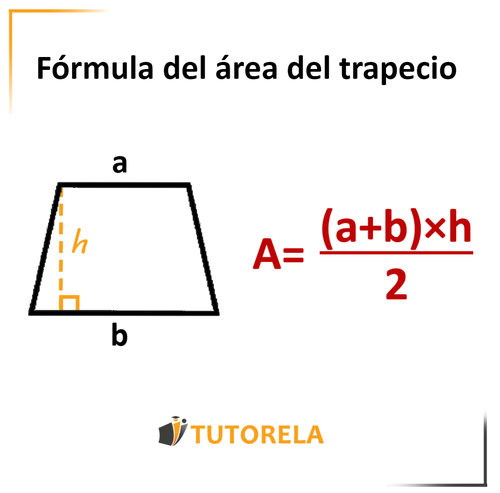
Sumaremos las bases y multiplicaremos el resultado por la altura del trapecio.
Dividiremos el resultado por .
Para obtener más información, ingresa al link de Área del trapecio
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Área del deltoide (o cometa)
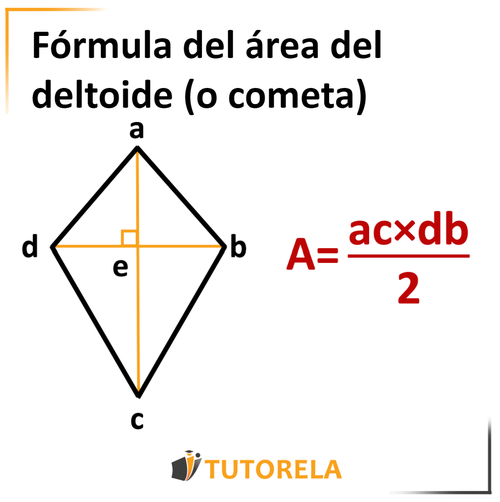
Multiplicaremos las diagonales y dividiremos por .
Para obtener más información, ingresa al link de Área del deltoide (o cometa)
Área de figuras compuestas
No tienes que preocuparte por este par de vocablos - figuras compuestas No se las llama compuestas por ser complicadas o difíciles, sino, son figuras compuestas porque realmente las componen varias figuras que tú ya conoces.
La gran clave para calcular el área de este tipo de figuras es separarlas en varias figuras simples sobre las que sabes calcular su área.
Veamos un ejemplo
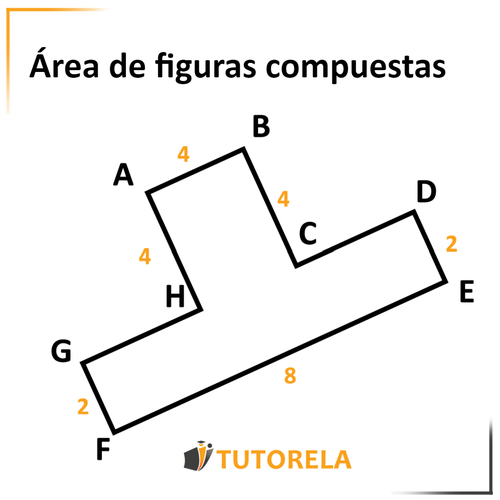
A primera vista podría asustarnos un poco ya que la figura parece muy rara. Pero, muy rápidamente recordaremos la sugerencia que hemos escrito aquí arriba y la aplicaremos.
Nos percataremos de que podemos dividir la figura compuesta en dos que nosotros conocemos y sabemos cómo calcular su área, rectángulo y cuadrado.
Calcularemos el área de cada figura por separado y luego las sumaremos.
De este modo obtendremos el área de toda la figura.
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Calcula el área del paralelogramo según los datos.
¿Qué diferencia hay entre superficie y volumen?
Para entender la diferencia recordemos un término diario que utilizamos en otro contexto: superficial.
Superficial implica algo o alguien sin profundidad, entonces, en geometría la superficie nos indica el tamaño de algo plano, sin profundidad. Por ejemplo, si dibujamos una pelota y la pintamos, esa parte pintada sería su superficie.
En cambio, el volumen se refiere al tamaño real de la pelota, el sitio que podríamos rellenar dentro de ella.
El volumen no es la superficie sobre la hoja de papel, sino, realmente el tamaño que podemos ver (de modo tridimensional) - el sitio que ocupa en el espacio.
El cálculo del volumen difiere del cálculo de la superficie.

Si te interesa este artículo también te pueden interesar los siguientes artículos
En Tutorela encontrarás una variedad de artículos sobre matemáticas.
Ejemplos y ejercicios con soluciones de cálculo de área
Ejercicio #1
Calcula el área del paralelogramo según los datos.
Solución en video
Solución Paso a Paso
Como sabemos que ABCD es un paralelogramo, según las propiedades del mismo todo par de lados opuestos son iguales y paralelos.
Por lo tanto
Calculamos el área del paralelogramo según la fórmula de lado por la altura que desciende de ese lado, por lo tanto el área del paralelogramo es igual a:
Respuesta
70
Ejercicio #2
Calcula el área del triángulo siguiente:
Solución en video
Solución Paso a Paso
La fórmula de cálculo del área triangular es:
(el lado * la altura del lado que desciende al lado) /2
Es decir:
Ahora reemplazamos los datos existentes:
Respuesta
10
Ejercicio #3
Dado el siguiente rectángulo:
Halla el área del rectángulo.
Solución en video
Solución Paso a Paso
Calculemos el área del rectángulo multiplicando el largo por el ancho:
Respuesta
10
Ejercicio #4
Dado el trapecio:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Fórmula del área de un trapecio:
Reemplazamos los datos en la fórmula y resolvemos:
Respuesta
52.5
Ejercicio #5
El ancho del rectángulo es igual a 15 cm y el largo es igual a 3 cm
Calcula el área del rectángulo
Solución en video
Solución Paso a Paso
Para calcular el área del rectángulo, multiplicamos el largo por el ancho:
Respuesta
45
Completa la oración
Para encontrar el área de un triángulo rectángulo, se debe multiplicar a _ entre sí y dividir por 2.
Indica la respuesta correcta
El cuadrilátero siguiente es:
Indica la respuesta correcta
El cuadrilátero siguiente es:
Más preguntas
Area of a Triangle
- Cálculo del Área de un Triángulo: Base 5 y Altura 6
- Cálculo del Área de un Triángulo Rectángulo: Lados 5, 7 y 8.6 Unidades
- Cálculo del Área del Triángulo ABC: AC=10cm, AD=3cm, BC=11.6cm
- Calcula la Altura X en un Triángulo Rectángulo con Área 20 y Base 5
- Área de Triángulo con Altura 7 y Base 8.5: ¿Es Posible Calcularlo?
- Líneas paralelas (Rectas paralelas)
- Ángulos en rectas paralelas
- Ángulos alternos
- Ángulos correspondientes
- Ángulos colaterales
- Ángulos opuestos por el vértice
- Ángulos adyacentes
- El Teorema de Pitágoras
- Altura del triángulo
- Elementos de la circunferencia
- Círculo
- Diámetro
- Pi
- Área de un circulo
- Distancia de la cuerda al centro del círculo
- Cuerdas en un círculo
- Ángulo central en un círculo
- Arcos en un círculo
- Perpendicular a la cuerda desde el centro del círculo
- Ángulo inscrito en un círculo
- Tangente de un círculo
- Perímetro de un circulo
- El centro de la circunferencia
- Radio
- ¿Cómo se calcula el radio mediante su circunferencia?
- Triángulos congruentes
- Deltoide
- Área del deltoide:
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Maneras de identificar paralelogramos
- Simetría rotacional en paralelogramos
- Del cuadrilátero al paralelogramo
- Semejanza de triángulos y polígonos
- Criterios de semejanza de triángulos
- Trapecios
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- Área de un trapecio
- Perímetro de un trapecio
- Trapecio isósceles
- Rectángulo
- De un cuadrilátero a un rectángulo
- Del paralelogramo al rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Cuadrado
- El área de un cuadrado
- De paralelogramo a cuadrado
- Segmento medio
- Segmento medio de un triángulo
- Segmento medio de un trapecio
- Área
- ¿Rombo, cometa o diamante?
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
- El área de un rombo
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Área del cilindro
- Volumen del cilindro
- Prisma rectangular (ortoedro)
- El cubo
- Cómo calcular el área de superficie de un prisma rectangular (ortoedro)
- Cómo calcular el volumen de un prisma rectangular (ortoedro)
- Área lateral de un ortoedro
- Prisma triangular recto
- Las bases del prisma triangular recto
- Las caras laterales del prisma
- Aristas laterales de un prisma
- Altura del prisma
- El volumen del prisma
- Área de superficie de prismas triangulares
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Ángulos exteriores correspondientes
- Ángulos alternos internos
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- Partes de un Círculo
- Componentes del Circuito
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









